
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )

A.3![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
【答案】B
【解析】
连接EG,由折叠的性质可得BE=EF又由E是BC边的中点,可得EF=EC,然后证得Rt△EGF≌Rt△EGC(HL),得出FG=CG=2,继而求得线段AG的长,再利用勾股定理求解,即可求得答案.
解:连接EG,
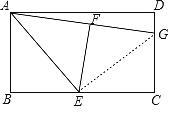
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=∠B=90°,
∵在Rt△EGF和Rt△EGC中,
![]() ,
,
∴Rt△EGF≌Rt△EGC(HL),
∴FG=CG=2,
∵在矩形ABCD中,AB=CD=CG+DG=2+1=3,
∴AF=AB=3,
∴AG=AF+FG=3+2=5,
∴BC=AD=![]() =
=![]() =2
=2![]() .
.
故选:B.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某汽车租赁公司要购买轿车和面包车共![]() 辆.其中面包车不能超过轿车的两倍,轿车每辆
辆.其中面包车不能超过轿车的两倍,轿车每辆![]() 万元,面包车每辆
万元,面包车每辆![]() 万元,公司可投入的购车款不超过61万元.
万元,公司可投入的购车款不超过61万元.
(小题1)符合公司要求的购买方案有哪几种?请说明理由.
(小题2)如果每辆轿车的日租金为![]() 元,每辆面包车的日租金为
元,每辆面包车的日租金为![]() 元.假设新购买的这
元.假设新购买的这![]() 辆车每日都可租出,要使这
辆车每日都可租出,要使这![]() 辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
辆车的日租金收入不低于1600元,那么应选择以上哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
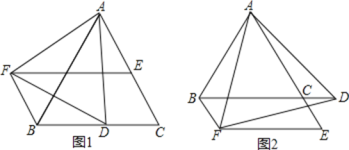
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.我们知道|a|的几何意义是指数轴上表示数的点与原点的距离,那么|a-b|的几何意义又是什么呢?我们不妨考虑一下,取特殊值时的情况.比如考虑|5-(-6)|的几何意义,在数轴上分别标出表示-6和5的点,(如图所示),两点间的距离是11,而|5-(-6)|=11,因此不难看出|5-(-6)|就是数轴上表示-6和5两点间的距离.
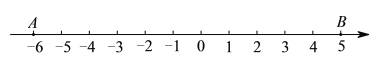
(1)|a-b|的几何意义是_______;
(2)当|x-2|=2时,求出x的值.
(3)设Q=|x+6|-|x-5|,请问Q是否存在最大值,若没有请说明理由,若有,请求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

(1)这8筐白菜中,最接近25千克的那筐白菜为______千克;
(2)以每筐25千克为标准,这8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )
A. 290×![]() B. 290×
B. 290×![]()
C. 2.90×![]() D. 2.90×
D. 2.90×![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com