
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
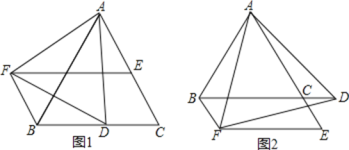
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
【答案】(1)见解析;(2) 四边形BCEF是平行四边形,理由见解析;(3) 成立,理由见解析.
【解析】
(1)利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC;
(2)四边形BCEF是平行四边形,因为△AFB≌△ADC,所以可得∠ABF=∠C=60°,进而证明∠ABF=∠BAC,则可得到FB∥AC,又BC∥EF,所以四边形BCEF是平行四边形;
(3)易证AF=AD,AB=AC,∠FAD=∠BAC=60°,可得∠FAB=∠DAC,即可证明△AFB≌△ADC;根据△AFB≌△ADC可得∠ABF=∠ADC,进而求得∠AFB=∠EAF,求得BF∥AE,又BC∥EF,从而证得四边形BCEF是平行四边形.
![]() 和
和![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ;
;
![]() 由
由![]() 得
得![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形BCEF是平行四边形;
四边形BCEF是平行四边形;
![]() 成立,理由如下:
成立,理由如下:
![]() 和
和![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]() ;
;
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形BCEF是平行四边形.
四边形BCEF是平行四边形.


科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(k≠0)与一次函数y=-x+5的一个交点是A(1,n).
(1)求反比例函数y=![]() (k≠0)的表达式;
(k≠0)的表达式;
(2)当一次函数的函数值大于反比例函数的函数值时,直接写出自变量x的取值范围为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )
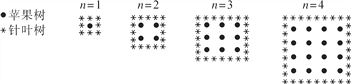
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
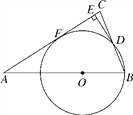
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )

A.3![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
调查结果统计表

调查结果频数分布直方图 调查结果扇形统计图

请根据以上图表,解答下列问题:
(1)填空:这次调查的样本容量是 ,![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(4)该校共有![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com