
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
【答案】(1)20°;(2)当∠AOC的度数是60°或108°时,∠COE=2∠DOB
【解析】
(1)依据邻补角的定义以及角平分线的定义,即可得到∠COE的度数,进而得出∠DOE的度数;
(2)设∠AOC=α,则∠BOC=180°-α,依据OE平分∠BOC,可得∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
(1)∵∠AOC=40°,
∴∠BOC=140°,
又∵OE平分∠BOC,
∴∠COE=![]() ×140°=70°,
×140°=70°,
∵∠COD=90°,
∴∠DOE=90°-70°=20°;
(2)设∠AOC=α,则∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,
α,
分两种情况:
当OD在直线AB上方时,∠BOD=90°-α,
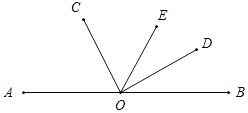
∵∠COE=2∠DOB,
∴90°-![]() α=2(90°-α),
α=2(90°-α),
解得α=60°.
当OD在直线AB下方时,∠BOD=90°-(180°-α)=α-90°,
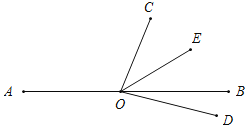
∵∠COE=2∠DOB,
∴90°-![]() α=2(α-90°),
α=2(α-90°),
解得α=108°.
综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB.


科目:初中数学 来源: 题型:
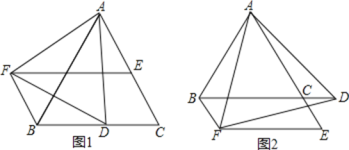
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )
A. 290×![]() B. 290×
B. 290×![]()
C. 2.90×![]() D. 2.90×
D. 2.90×![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
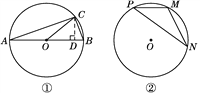
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=![]() ,求sin 2α的值.
,求sin 2α的值.
小娟是这样给小芸讲解的:
如图①,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°. 设∠BAC=α,则sin α=![]() =
=![]() .易得∠BOC=2α.设BC=x,则AB=3x,AC=2
.易得∠BOC=2α.设BC=x,则AB=3x,AC=2![]() x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=
x.作CD⊥AB于D,求出CD=________(用含x的式子表示),可求得sin 2α=![]() =________.
=________.
【问题解决】已知,如图②,点M,N,P为⊙O上的三点,且∠P=β,sin β=![]() ,求sin 2β的值.
,求sin 2β的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的程序表示,输入一个整数![]() 便会按程序进行计算.
便会按程序进行计算.

设输入的![]() 值为
值为![]() ,那么根据程序,第
,那么根据程序,第![]() 次计算的结果是
次计算的结果是![]() ;第
;第![]() 次计算的结果是
次计算的结果是![]() ,这样下去第5次计算的结果是__________,第2019次计算的结果是______________.
,这样下去第5次计算的结果是__________,第2019次计算的结果是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,延长AB到点C,使得2BC=3OB,D是⊙O上一点,连接AD,CD,过点A作CD的垂线,交CD的延长线于点F,过点D作DE⊥AC于点E,且DE=DF.
(1)求证:CD是⊙O的切线;
(2)若AB=4.
①求DF的长;
②连接OF,交AD于点M,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
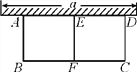
【题目】如图,有长为24 m的篱笆,一面利用墙(墙的最大可用长度a为10 m)围成中间隔着一道篱笆的长方形花圃.
(1)现要围成面积为45 m2的花圃,则AB的长是多少米?
(2)现要围成面积为48 m2的花圃能行吗?若能行,则AB的长是多少?若不能行,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com