练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）-12017+(π-3)0+（-）

    （2）(-a)3a2+(2a4)2÷a3

    （3） 6 (-x2-xy+y2）（-xy）

    （4） x2-(x+2) (x-2)

    【答案】（1）-；（2）3a5；（3）6x3y+6x2y2-6xy3；（4）4

    【解析】

    （1）先进行0次幂运算，再按运算顺序进行计算即可；

    （2）先计算积的乘方，再按照整式乘除计算，最后合并同类项即可；

    （3）按照单项式乘多项式法则依次计算即可；

    （4）先用平方差计算，再合并同类项即可.

    解：（1）原式=-1+1-

    =-

    （2）原式=-a5+4a8÷a3

    =-a5+4a5

    =3a5

    （3）原式= (-6x2-6xy+6y2）（-xy）

    = 6x3y+6x2y2-6xy3

    （4）原式= x2-（x2-4）

    =4

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．

    （1）求C点坐标；

    （2）求直线MN的解析式；

    （3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A是反比例函数y＝（m＜0）位于第二象限的图像上的一个动点，过点A作AC⊥x

    轴于点C；M为是线段AC的中点，过点M作AC的垂线，与反比例函数的图像及y轴分别交于B、

    D两点．顺次连接A、B、C、D．设点A的横坐标为n．

    （1）求点B的坐标（用含有m、n的代数式表示）；

    （2）求证：四边形ABCD是菱形；

    （3）若△ABM的面积为2，当四边形ABCD是正方形时，求直线AB的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车租赁公司要购买轿车和面包车共辆．其中面包车不能超过轿车的两倍，轿车每辆万元，面包车每辆万元，公司可投入的购车款不超过61万元．

    （小题1）符合公司要求的购买方案有哪几种？请说明理由．

    （小题2）如果每辆轿车的日租金为元，每辆面包车的日租金为元．假设新购买的这辆车每日都可租出，要使这辆车的日租金收入不低于1600元，那么应选择以上哪种购买方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图象（折线OEFPMN）描述了某汽车在行驶过程中速度与时间的函数关系，下列说法中错误的是（ ）

    A. 第3分时汽车的速度是40千米/时

    B. 第12分时汽车的速度是0千米/时

    C. 从第3分到第6分，汽车行驶了120千米

    D. 从第9分到第12分，汽车的速度从60千米/时减少到0千米/时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

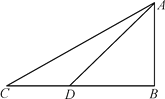
    【题目】如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30，再向旗杆的方向前进16米，到达点D处(C，D，B三点在同一直线上)，又测得旗杆顶端A的仰角为45，请计算旗杆AB的高度(结果保留根号)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）若a2＝16，|b|＝3，且ab＜0，求a+b的值；

    （2）已知a、b互为相反数且a≠0，c、d互为倒数，m的绝对值是5，求m2﹣（﹣1）+（a+b）﹣cd的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，他这天下午行驶里程如下：（单位：千米）

    +15, -3, +14，-11，+10，-12，+4，-15，+16，-18

    （1）他将最后一名乘客送到目的地时，距下午出车地点是多少千米？

    （2）若汽车耗油量为升∕千米，这天下午共耗油多少升

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知矩形ABCD，AB＝6，AD＝8，将矩形ABCD绕点A顺时针旋转θ（0°＜θ＜360°）得到矩形AEFG，当θ＝_____°时，GC＝GB．

    查看答案和解析>>

    同步练习册答案