
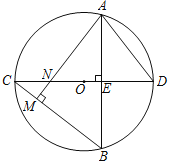
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)先根据圆周角定理得出∠BAD=∠BCD,再由直角三角形的性质得出∠ANE=∠CNM,故可得出∠BCD=∠BAM,由全等三角形的判定定理得出△ANE≌△ADE,故可得出结论;
(2)先根据垂径定理求出AE的长,设NE=x,则OE=x-1,NE=ED=x,r=OD=OE+ED=2x-1
连结AO,则AO=OD=2x-1,在Rt△AOE中根据勾股定理可得出x的值,进而得出结论.
试题解析:
(1)证明:∵CD⊥AB
∴∠CEB=90
∴∠C+∠B=90.
同理∠C+∠CNM=90
∴∠CNM=∠B.
∵∠CNM=∠AND
∴∠AND=∠B
∵弧AC=弧AC
∴∠D=∠B
∴∠AND=∠D
∴AN=AD
(2)解:设ON的长为![]() ,连接OA
,连接OA
∵AN=AD,CD⊥AB
∴DE=NE= ![]()
∴OD=OE+ED= ![]()
∴OA=OD![]() .
.
∴在Rt△OAE中![]()
∴![]()
解得![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去).
∴OA![]() .
.
即⊙O的半径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论①AS=AR;②QP∥AR;③△BRP≌△CQP中( ) 
A.全部正确
B.仅①和②正确
C.仅①正确
D.仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
A.AE=6cm
B.sin∠EBC= ![]()
C.当0<t≤10时,y= ![]() t2
t2
D.当t=12s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
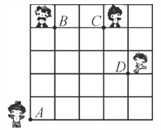
【题目】如图,奥运福娃在5×5的方格(每小格边长为1 m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其他福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A·B(+1,+4),从B到A记为:B·A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中:
(1)A·C(__________,__________),B·C(__________,__________),C·__________(-3,-4);
(2)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出妮妮的位置点E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若方程(a+2)x=2的解为x=2,想一想不等式(a+4)x>-3的解集是多少?试判断-2,-1,0,1,2,3这6个数中哪些数是该不等式的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一时刻,两根长度不等的竿子置于阳光之下,而它们的影长相等,那么这两根竿子的相对位置是( )
A. 两根都垂直于地面B. 两根平行斜插在地上C. 两根不平行D. 两根平行倒在地上
查看答案和解析>>
科目:初中数学 来源: 题型:
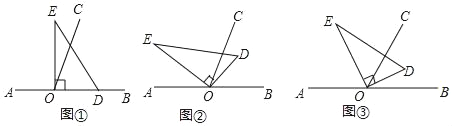
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com