
����Ŀ����ͼ����ֱ��AB��һ��OΪ�˵�������OC��ʹ��BOC=70������һ��ֱ�������ε�ֱ�Ƕ�����ڵ�O������ע����DOE=90�㣩
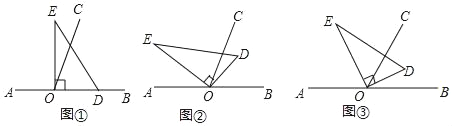
��1����ͼ�٣���ֱ�����ǰ�DOE��һ��OD��������OB�ϣ����COE=�� ���㣻
��2����ͼ�ڣ���ֱ�����ǰ�DOE�Ƶ�O��ʱ�뷽��ת����ij��λ�ã���OCǡ��ƽ�֡�BOE�����COD�Ķ�����
��3����ͼ�ۣ���ֱ�����ǰ�DOE�Ƶ�Oת�������ODʼ���ڡ�BOC���ڲ����Բ����BOD�͡�COE��������������ϵ����˵�����ɣ�
���𰸡���1��20����2��20 ����3����COE����BOD=20�㣮
�������������������1������ͼ�εó���COE=��DOE-��BOC������������ɣ���2�����ݽ�ƽ���߶��������EOB=2��BOC=140�㣬�����BOD=��BOE-��DOE�������BOD�������COD=��BOC-��BOD������ɣ���3������ͼ�εó���BOD+��COD=��BOC=70�㣬��COE+��COD=��DOE=90�㣬�����������𰸣�
���������
��1����ͼ�٣���COE=��DOE����BOC=90�㩁70��=20�㣻
��2����ͼ�ڣ���OCƽ����EOB����BOC=70�㣬
���EOB=2��BOC=140�㣬
�ߡ�DOE=90�㣬
���BOD=��BOE����DOE=50�㣬
�ߡ�BOC=70�㣬
���COD=��BOC����BOD=20�㣻
��3����COE����BOD=20�㣬
�����ǣ���ͼ�ۣ��ߡ�BOD+��COD=��BOC=70�㣬��COE+��COD=��DOE=90�㣬
�ࣨ��COE+��COD��������BOD+��COD��
=��COE+��COD����BOD����COD
=��COE����BOD
=90�㩁70��
=20�㣬
����COE����BOD=20�㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������������������С������ĵڶ���,Ϊ�˸��õ����á������������С�����,�н�������ز��Ŷ�ij��ѧѧ�������ġ���֪����,��ȡ��������ķ��������ʾ�����,��������Ϊ���dz��˽⡱, ����У�˽⡱, �������˽⡱,�͡����˽⡱�ĸ��ȼ�.С�Ը��ݵ�������������ͼ��ʾ��ͳ��ͼ,������ṩ����Ϣ�ش�����:

(1)�������,����������_________;
(2)����ͳ��ͼ�С������˽⡱��������Ӧ��Բ�ĽǵĶ�����_______;�ڸ�У2000��ѧ�����������һ��ѧ��,�ԡ����ġ����˽�ĸ��ʹ���ֵΪ________
(3)�벹ȫƵ���ֲ�ֱ��ͼ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
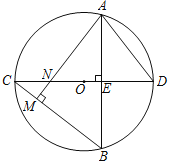
����Ŀ����ͼ,��O��,ֱ��CD����AB��E,AM��BC��M,��CD��N,����AD.
(1)��֤:AD=AN;
(2)��AB=8,ON=1,���O�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ,ֱ��![]() �������ύ�ڵ�A,C,������A,C��������y=ax2+bx-3��x�ύ�ڵ�B(2��0).
�������ύ�ڵ�A,C,������A,C��������y=ax2+bx-3��x�ύ�ڵ�B(2��0).
(1)�������ߵĽ���ʽ;
(2)��D���������ڵ�������ͼ���ϵĶ���,�Ƿ���ڵ�D,ʹ�á�DAC��������,������,����������ֵ�������D������;��������,��˵������;
(3)����D��DE��x����E,��AC��F,��ACǡ�ý���ADE������ֳ�1:4������,�������ʱ��D������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����У���ȷ����( )
A. 6a+4b��10abB. 7x2y��3x2y��4x4y2
C. 7a2b��7ba2��0D. 8x2+8x2��16x4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����У���ȷ���ǣ� ��
A.a3+a3=a6
B.��a2��3=a5
C.a2a4=a8
D.a4��a3=a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ݣ���4¥9�ţ��ڱ�ƫ��20�㣻�۽�̫·3�ţ��ܶ���108�㣬��γ30�㣬����ȷ������λ�õ���( )
A. �٢� B. �ڢ�
C. �� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AC��BD���ڵ�O����OA=OC��������һ��������ʹ��OAB�ա�OCD����������� �� 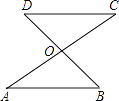
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com