
【题目】已知:如图,直线![]() 与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大,若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.

【答案】(1)![]() ;(2)存在,D
;(2)存在,D![]() ,最大值为
,最大值为![]() ;(3)D
;(3)D![]()
【解析】试题分析:(1)利用一次函数求出点A的坐标,把A、B的坐标代入二次函数解析式即可;(2)设出点D的坐标,再把点F的坐标代入AC求出,△DAC的面积=△DAF的面积+△DFC的面积,即可求出面积的最大值;(3)AC恰好将△ADE的面积分成1:4两部分,所以出现两种情况:DF:EF=1:4, DF:EF=4:1,分类讨论即可.
试题解析:
(1)在![]() 中,当
中,当![]() ,即点A的坐标为
,即点A的坐标为![]()
将A![]() ,B
,B![]() 代入
代入![]() 得
得
![]()
解得![]()
∴抛物线的解析式为: ![]()
(2)设点D的坐标为![]() ,则点F的坐标为
,则点F的坐标为![]()
∴DF= ![]()
∴![]()
![]()
![]()
∵![]() 抛物线开口向下
抛物线开口向下
∴当![]() 时,
时, ![]() 存在最大值
存在最大值![]()
又∵当![]() 时,
时, ![]()
∴存在点D![]() ,使得△ADC的面积最大,最大值为
,使得△ADC的面积最大,最大值为![]()
(3)由题意可得△ADE的面积分成1:4两部分即是点F将DE分成1:4两部分
①当DF:EF=1:4时![]()
解得![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
当![]() 时,
时, ![]()
∴点D的坐标为![]()
②当DF:EF=4:1时![]()
解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() (不合题意,舍去)
(不合题意,舍去)
综上所述存在点D![]() 使得AC恰好将△ADE的面积分成1:4两部分
使得AC恰好将△ADE的面积分成1:4两部分


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
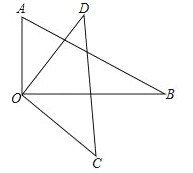
【题目】如图,将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)若∠BOD=35°,则∠AOC= ;
(2)若∠AOC=135°,则∠BOD= ;
(3)猜想∠AOC与∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A. 3x+x=3x2B. ﹣2a+5b=3ab
C. 4m2n+2mn2=6mnD. 3ab2﹣5b2a=﹣2ab2
查看答案和解析>>
科目:初中数学 来源: 题型:
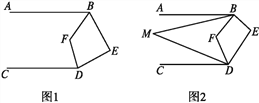
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3,4三个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤9,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
A.5
B.4或5
C.5或6
D.6或7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com