
【题目】已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于点F.
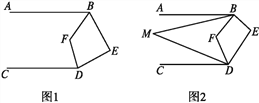
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2,若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
∠CDF,试写出∠M与∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
∠CDF,∠E=m°,请直接用含有n,m°的代数式表示出∠M.
【答案】(1)∠BFD=140°;(2)6∠M+∠E=360°;(3)![]() .
.
【解析】(1)首先作EG∥AB,FH∥AB,利用平行线的性质可得∠ABE+∠CDE=280°,再利用角平分线的定义得到∠ABF+∠CDF=140°,从而得到∠BFD的度数;
(2)先由已知得到∠ABE=6∠ABM,∠CDE=6∠CDM,由(1)得∠ABE+∠CDE=360°-∠E,∠M=∠ABM+∠CDM,等量代换,即可;
(3)由(2)的方法可得到2n∠M+∠E=360°,将∠E=m°代入可得∠M=![]() .
.
解:(1)作EG∥AB,FH∥AB,因为AB∥CD,
所以EG∥AB∥FH∥CD.
所以∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,所以∠ABE+∠BEG+∠GED+∠CDE=360°.
因为∠BED=∠BEG+∠DEG=80°,
所以∠ABE+∠CDE=280°.
因为∠ABE和∠CDE的角平分线相交于点F,
所以∠ABF+∠CDF=140°,
所以∠BFD=∠BFH+∠DFH=140°.
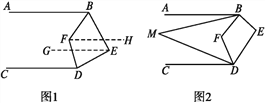
(2)因为∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,所以∠ABF=3∠ABM,∠CDF=3∠CDM,因为∠ABE与∠CDE两个角的角平分线相交于点F,
∠CDF,所以∠ABF=3∠ABM,∠CDF=3∠CDM,因为∠ABE与∠CDE两个角的角平分线相交于点F,
所以∠ABE=6∠ABM,∠CDE=6∠CDM,
所以6∠ABM+6∠CDM+∠E=360°.
因为∠M=∠ABM+∠CDM,
所以6∠M+∠E=360°.
(3)由(2)结论可得,
2n∠ABM+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
解得∠M=![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大,若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图用点A(3,1)表示放置3个胡萝卜、1棵青菜,点B(2,3)表示放置2个胡萝卜、3棵青菜.

(1)请你写出其他各点C,D,E,F所表示的意义;
(2)若一只兔子从A到达B(顺着方格线走),有以下几条路可以选择:①A→C→D→B;②A→F→D→B;③A→F→E→B,帮可爱的小白兔选一条路,使它吃到的食物最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五子连珠棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记作(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某省商务厅最新消息,2018年第一季度该省企业对“一带一路”沿线国家的投资额为10亿美元,第三季度的投资额增加到了14.4亿美元.求该省第二、三季度投资额的平均增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com