
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 所在的直线上运动,作
所在的直线上运动,作![]() (
(![]() 、
、![]() 、
、![]() 按逆时针方向).
按逆时针方向).
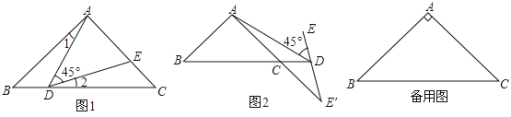
(1)如图①,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 交
交![]() 于
于![]() .
.
①求证:![]() .
.
②当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
(2)如图②,当点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的反向延长线与
的反向延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,写出点
是等腰三角形?若存在,写出点![]() 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
【答案】(1) ①证明见解析;②AE的值是1或 2或![]() ; (3)存在,D在BC的延长线上,且CD= 2
; (3)存在,D在BC的延长线上,且CD= 2
【解析】
(1) ①求出∠B=45°,根据三角形外角性质得出∠1+∠B=∠ADC=45°+∠2.求出即可;
②分为三种情况,①DE=AE,②AD=AE,③AD=DE,根据等腰三角形性质(等腰三角形两边相等),三角形全等推出即可;
(2)存在,可证![]() 得到CD=AC=2.
得到CD=AC=2.
解(1) ①∵在Rt△ABC中,∠BAC=90°。AB=AC,
∴∠B=∠C=45°
∵∠ADE=45°,
∴∠ADC=∠B+∠1=∠ADE+∠2,
即45°+∠1=45°+∠2.
∴∠1=∠2.
②解:当△ADE是等腰三角形时,分为以下三种情况:
第一种情况: DE=AE,

∵DE=AE,
∴∠ADE=∠DAE=45°=∠C,
∴∠AED=90°,∠ADC=90° ,
即DE⊥.AC.
∴AD= DC.
∴E为AC的中点,
∴![]()
第二种情况: AD=AE,此时D和B重合,E和C重合,

即AE=AC=2;
第三种情况: AD=DE,
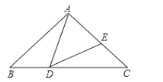
在△ABD和△DCE中.
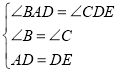
∴![]() ,
,
∴BD=CE,AB=DC,
设BD=CE=x,
在Rt△ABC中,∵∠BAC=90°, AB=AC=2,
∴BC=![]() .
.
∴DC=![]() -x.
-x.
∴![]() -x=2,
-x=2,
∴x=![]() -2,
-2,
∴AE=![]()
综合上述: AE的值是1或 2或![]()
(3)解:存在,理由如下:
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴![]()
又∵![]() ,
,
∴![]() ,
,
故存在点![]() ,使
,使![]() 是等腰三角形,此时D在BC的延长线上,且CD= 2
是等腰三角形,此时D在BC的延长线上,且CD= 2


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,P是直线AC上一点,AD⊥BP于D,以AD为边作等边△ADE(D,E在直线AC异侧).
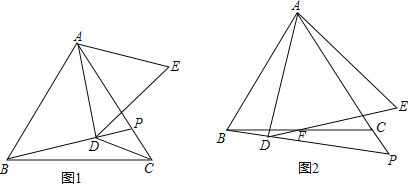
(1)如图1,若点P在边AC上,连CD,且∠BDC=150°,则![]() = ;(直接写结果)
= ;(直接写结果)
(2)如图2,若点P在AC延长线上,DE交BC于F求证:BF=CF;
(3)在图2中,若∠PBC=15°,AB=![]() ,请直接写出CP的长 .
,请直接写出CP的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
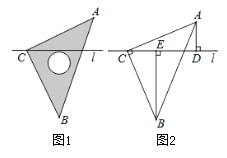
(1)△ACD与△CBE全等吗?说明你的理由.
(2)若AD=2,DE=3.5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B= 60°.
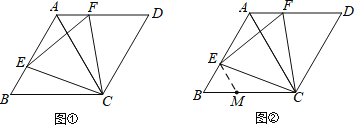
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△OAB的顶点A(6,0),B(0,2),O是坐标原点.将△OAB 绕点O按逆时针旋转90°得到△ODC.
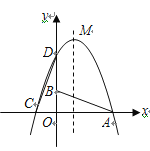
(1)写出C、D两点的坐标;
(2)求过C、D、A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得MA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
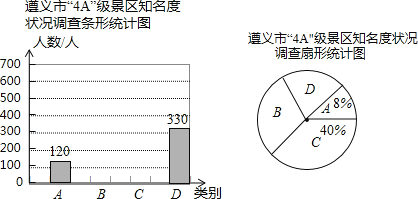
【题目】今年5月,从全国旅游景区质量等级评审会上传来喜讯,我市“风冈茶海之心”、赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区.至此,全市“4A”级景区已达13个.某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,按答数多少分为熟悉(A),基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了一下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)调查中属于“基本了解”的市民有 人;
(3)补全条形统计图;
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
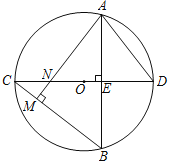
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
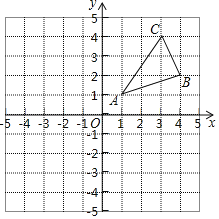
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)作出与△ABC关于y轴对称△A1B1C1,并写出三个顶点的坐标为:A1(_____),B1(______),C1(_______);
(2)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com