
【题目】今年5月,从全国旅游景区质量等级评审会上传来喜讯,我市“风冈茶海之心”、赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区.至此,全市“4A”级景区已达13个.某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,按答数多少分为熟悉(A),基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了一下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)调查中属于“基本了解”的市民有 人;
(3)补全条形统计图;
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
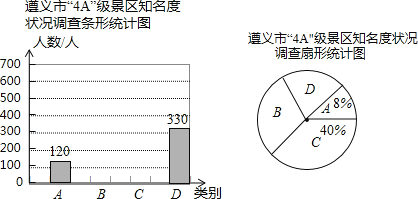
【答案】(1)1500;(2)45;(3)补图见解析;(4)“略有知晓”类占扇形统计图的圆心角是144°,“知之甚少”类市民占被调查人数的百分比是22%.
【解析】
(1)用熟悉(A)的人数除以所占的百分比,计算即可得解;
(2)先求出略有知晓(C)的人数,然后列式计算即可得解;
(3)根据(2)的计算补全图形统计图即可;
(4)用“略有知晓”C所占的百分比乘以360°计算即可,再根据知之甚少(D)的人数列式计算即可求出所占的百分比.
(1)120÷8%=1500;
(2)略有知晓(C)的人数为:1500×40%=600人,
“基本了解”(B)的人数为:1500-120-600-330=1500-1050=450人;
(3) 补全统计图如图所示;

(4)“略有知晓”类占扇形统计图的圆心角是:360°×40%=144°
“知之甚少”类市民占被调查人数的百分比是: ![]() ×100%=22%.
×100%=22%.


科目:初中数学 来源: 题型:
【题目】将矩形纸片分别沿两条不同的直线剪两刀,可以使剪得的三块纸片恰能拼成一个等腰三角形(不能有重叠和缝隙).小华的做法是:如图1所示,在矩形ABCD中,分别取AD、AB、CD的中点P、E、F,并沿直线PE 、PF剪两刀,所得的三部分可拼成等腰三角形△PMN (如图2).
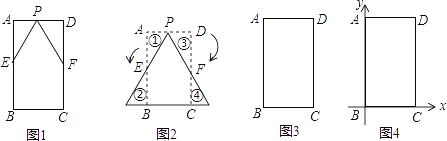
(1)在图3中画出另一种剪拼成等腰三角形的示意图;
(2)以矩形ABCD的顶点B为原点,BC所在直线为x轴建立平面直角坐标系(如图4),矩形ABCD剪拼后得到等腰三角形△PMN,点P在边AD上(不与点A、D重合),点M、N在x轴上(点M在N的左边).如果点D的坐标为(5,8),直线PM的解析式为y=kx+b,求所有满足条件的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
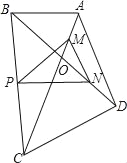
【题目】在△AOB中,AB=OB=2,△COD中,CD=OC=3,∠ABO=∠DCO.连接AD、BC,点M、N、P分别为OA、OD、BC的中点.
①若A、O、C三点在同一直线上,且∠ABO=2α,则![]() =_____(用含有α的式子表示);
=_____(用含有α的式子表示);
②固定△AOB,将△COD绕点O旋转,PM最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 所在的直线上运动,作
所在的直线上运动,作![]() (
(![]() 、
、![]() 、
、![]() 按逆时针方向).
按逆时针方向).
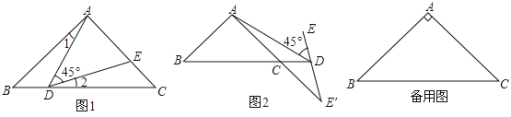
(1)如图①,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 交
交![]() 于
于![]() .
.
①求证:![]() .
.
②当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
(2)如图②,当点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的反向延长线与
的反向延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,写出点
是等腰三角形?若存在,写出点![]() 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为A的抛物线y=a(x- ![]() )2-2经过点B(-
)2-2经过点B(- ![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的解析式;
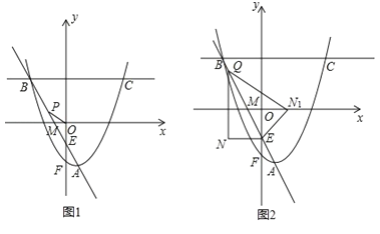
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
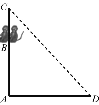
【题目】如图所示,AC是一根垂直于地面的木杆,B是木杆上的一点,且AB=2米,D是地面上一点,AD=3米.在B处有甲、乙两只猴子,D处有一堆食物.甲猴由B往下爬到A处再从地面直奔D处,乙猴则向上爬到木杆顶C处腾空直扑到D处,如果两猴所经过的距离相等,则木杆的长为( )
A. ![]() m B. 2
m B. 2![]() m C. 3
m C. 3![]() m D. 5 m
m D. 5 m
查看答案和解析>>
科目:初中数学 来源: 题型:
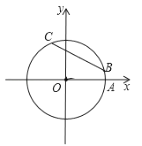
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(![]() ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com