
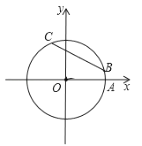
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(![]() ,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
,0),直线y=kx-2k+3与⊙O交于B、C两点,则弦BC的长的最小值为_______.
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
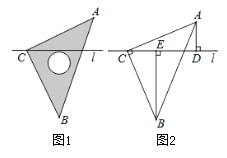
(1)△ACD与△CBE全等吗?说明你的理由.
(2)若AD=2,DE=3.5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
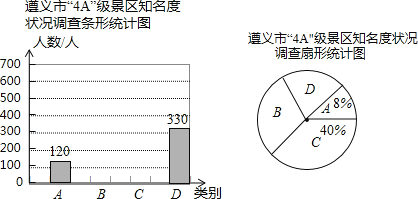
【题目】今年5月,从全国旅游景区质量等级评审会上传来喜讯,我市“风冈茶海之心”、赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区.至此,全市“4A”级景区已达13个.某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,按答数多少分为熟悉(A),基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了一下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)调查中属于“基本了解”的市民有 人;
(3)补全条形统计图;
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
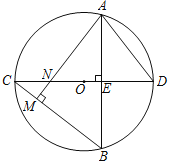
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
(1)求证:△AED≌△CFB;
(2)求证:四边形AFCE是平行四边形
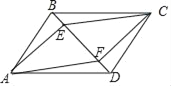
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)作出与△ABC关于y轴对称△A1B1C1,并写出三个顶点的坐标为:A1(_____),B1(______),C1(_______);
(2)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
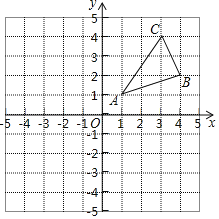
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
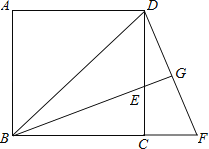
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com