
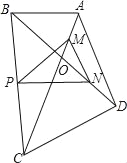
【题目】在△AOB中,AB=OB=2,△COD中,CD=OC=3,∠ABO=∠DCO.连接AD、BC,点M、N、P分别为OA、OD、BC的中点.
①若A、O、C三点在同一直线上,且∠ABO=2α,则![]() =_____(用含有α的式子表示);
=_____(用含有α的式子表示);
②固定△AOB,将△COD绕点O旋转,PM最大值为_____.
【答案】2sinα ![]()
【解析】
(1)连接BM、CN,则BM⊥OA,CN⊥OD,由四点共圆的判定知点B、C、M、N在以BC为直径的圆,且有MP=PN=BC÷2,而MN是△AOD的中位线,有MN等于AD的一半,故AD:BC=MN:PM,而可求得△PMN∽△BAO,有MN:PN=AO:AB=2sinα,从而求得AD:BC的值;
(2)取BO中点G,连接PG,MG,根据三角形中位线性质得PG=![]() OC=
OC=![]() ,GM=
,GM=![]() AB=1,利用三角形三边的关系得PM≤GP+GM,所以当M,P,G共线的时候PM最大=1+1.5=2.5.
AB=1,利用三角形三边的关系得PM≤GP+GM,所以当M,P,G共线的时候PM最大=1+1.5=2.5.
连接BM、CN.
∵AB=OB,M为OA的中点,∴BM⊥OA,∠AOB=∠COD=90°﹣α.同理CN⊥OD.
∵A、O、C三点在同一直线上,∴B、O、D三点也在同一直线上,∴∠BMC=∠CNB=90°.
∵P为BC中点,∴在Rt△BMC中,PM=![]() BC.在Rt△BNC中,PN=
BC.在Rt△BNC中,PN=![]() BC,∴PM=PN,∴B、C、N、M四点都在以点P为圆心,
BC,∴PM=PN,∴B、C、N、M四点都在以点P为圆心,![]() BC为半径的圆上,∴∠MPN=2∠MBN.
BC为半径的圆上,∴∠MPN=2∠MBN.
又∵∠MBN=![]() ∠ABO=α,∴∠MPN=∠ABO,∴△PMN∽△BAO,∴
∠ABO=α,∴∠MPN=∠ABO,∴△PMN∽△BAO,∴![]() ,由题意知MN=
,由题意知MN=![]() AD,PM=
AD,PM=![]() BC,∴
BC,∴![]() ,∴
,∴![]() .在Rt△BMA中,
.在Rt△BMA中,![]() sinα.
sinα.
∵AO=2AM,∴![]() =2sinα,∴
=2sinα,∴![]() =2sinα;
=2sinα;
(2)取BO中点G,连接PG,MG,则PG=![]() OC=
OC=![]() ,GM=
,GM=![]() AB=1,利用三角形三边的关系得PM≤GP+GM,所以当M,P,G共线的时候PM最大=1+1.5=2.5.
AB=1,利用三角形三边的关系得PM≤GP+GM,所以当M,P,G共线的时候PM最大=1+1.5=2.5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径圆弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED=![]() AB中,一定正确的是( )
AB中,一定正确的是( )
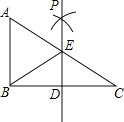
A.①②③ B.①②④ C.①③④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,,
,,![]()
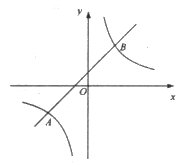
(1)求反比例函数与一次函数的函数表达式
(2)请结合图像直接写出不等式![]() 的解集;
的解集;
(3)若点P为x轴上一点,△ABP的面积为10,求点P的坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
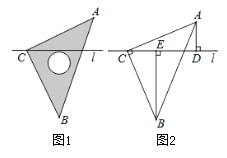
(1)△ACD与△CBE全等吗?说明你的理由.
(2)若AD=2,DE=3.5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 和
和![]() 交于点
交于点![]() .
.

(1)求证:![]() ;
;
(2)下列结论中,正确的有________个.
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .
.
(3)请选择(2)中任一正确结论进行证明.你选的序号是 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
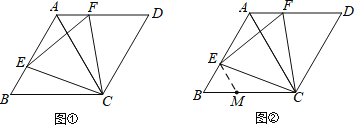
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
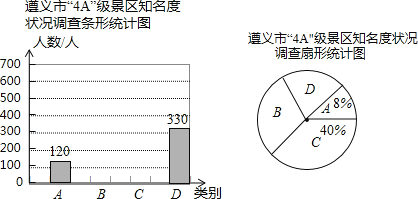
【题目】今年5月,从全国旅游景区质量等级评审会上传来喜讯,我市“风冈茶海之心”、赤水佛光岩”、“仁怀中国酒文化城”三个景区加入国家“4A”级景区.至此,全市“4A”级景区已达13个.某旅游公司为了了解我市“4A”级景区的知名度情况,特对部分市民进行现场采访,根据市民对13个景区名字的回答情况,按答数多少分为熟悉(A),基本了解(B)、略有知晓(C)、知之甚少(D)四类进行统计,绘制了一下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)调查中属于“基本了解”的市民有 人;
(3)补全条形统计图;
(4)“略有知晓”类占扇形统计图的圆心角是多少度?“知之甚少”类市民占被调查人数的百分比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com