
【题目】如图,已知△OAB的顶点A(6,0),B(0,2),O是坐标原点.将△OAB 绕点O按逆时针旋转90°得到△ODC.
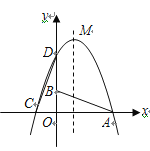
(1)写出C、D两点的坐标;
(2)求过C、D、A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得MA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】C(-2,0),D(0,6);(2)![]() ,M(2,8);(3)存在,N(0,2).
,M(2,8);(3)存在,N(0,2).
【解析】
(1)根据旋转的性质,可得OC=OB,OD=OA,进而可得CD两点的坐标;
(2)设出解析式,并将A、C、D三点的坐标代入可得方程组,解可得解析式,进而可得M的坐标;
(3)假设存在并设出其坐标,连接MB,作ME⊥y轴于E,可得ME、BE、MB的长,进而可得BA与MB的关系,即可求出N的坐标,故可作出判断.
(1)C(2,0),D(0,6).
(2)设所求抛物线的解析式为![]()
∵A,C,D在抛物线上
∴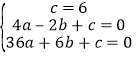 解得
解得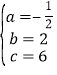 即
即 ![]()
又![]()
![]()
∴M(2,8).
(3) 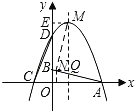
连接MB,作ME⊥y轴于E
则ME=2,BE=82=6
∴MB= ![]() ,BA=MB
,BA=MB
即在线段AB上存在点N(0,2)(即点B)使得NA=NM.


科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线交AD于E,交AC于F,∠CAD的角平分线AG交BF于H,交DC于G.

(1)求证:AE=AF;
(2)判断BF与AG的位置关系,并说明理由.
(3)再找出二组相等的线段:① ; ② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:等腰三角形腰上的高与底边的夹角等于其顶角的一半.
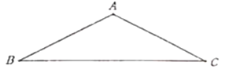
(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言写出“求证”.
已知:在![]() 中,
中,![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
求证:_____________________________________________________.
(2)证明上述命题:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 所在的直线上运动,作
所在的直线上运动,作![]() (
(![]() 、
、![]() 、
、![]() 按逆时针方向).
按逆时针方向).
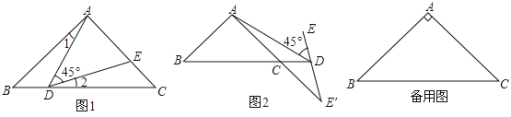
(1)如图①,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 交
交![]() 于
于![]() .
.
①求证:![]() .
.
②当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
(2)如图②,当点![]() 在
在![]() 的延长线上运动,
的延长线上运动,![]() 的反向延长线与
的反向延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 是等腰三角形?若存在,写出点
是等腰三角形?若存在,写出点![]() 的位置;若不存在,请简要说明理由.
的位置;若不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
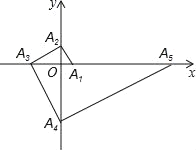
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2垂足为A2,交x轴于点A3过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4,过点A4作A4A5⊥A3A4,垂足为A4…交x轴于点A5:过点A5作A5A6⊥A4A5,A5A6⊥A4A5垂足为A5,交y轴于点A6…按此规律进行下去,则点A2019的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
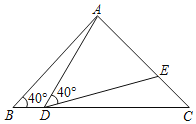
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.
(1)当∠BDA=115°时,∠BAD=_____°,∠DEC=_____°;当点D从B向C运动时,∠BDA逐渐变______(填”大”或”小”);
(2)当DC=AB=2时,△ABD与△DCE是否全等?请说明理由:
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com