
【题目】已知,如图,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线交AD于E,交AC于F,∠CAD的角平分线AG交BF于H,交DC于G.

(1)求证:AE=AF;
(2)判断BF与AG的位置关系,并说明理由.
(3)再找出二组相等的线段:① ; ② .
【答案】(1)见解析;(2)BF⊥AG,理由见解析;(3)EH=FH,BA=BG
【解析】
(1)根据等角的余角相等,得到∠AFB=∠BED,则∠AFB=∠AEF,即可得到AE=AF;
(2)由AE=AF,AG平分∠CAD,由三线合一定理,得到AH是等腰三角形AEF的高,即BF⊥AG;
(3)由(2)知△AEF是等腰三角形,则EH=FH,由BH是△ABG的边AG上的高,也是角平分线,则BA=BG.
解:(1)∵∠BAC=90°,AD⊥BC于D,
∴∠ABF+∠AFB=∠CBF+∠BED=90°,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠AFB=∠BED,
∵∠BED=∠AEF,
∴∠AFB=∠AEF,
∴AE=AF;
(2)在△AEF中,AE=AF,
∵AG平分∠CAD,
即AH平分∠FAE,
∴AH是等腰三角形AEF的高,
∴BF⊥AG;
(3)由(2)知,△AEF是等腰三角形,
∵AH⊥EF,
∴EH=FH,
∵BF⊥AG,BF平分∠ABC,
∴△ABG是等腰三角形,
∴AB=BG.
故答案为:EH=FH,AB=BG.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
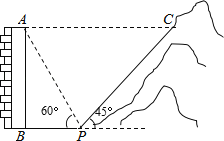
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
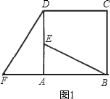
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 延长线上的一点,
延长线上的一点,![]() .
.
![]() 求证
求证![]() ;
;
![]() 阅读下列材料:
阅读下列材料:
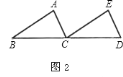
如图![]() ,把
,把![]() 沿直线
沿直线![]() 平行移动线段
平行移动线段![]() 的长度,可以变到
的长度,可以变到![]() 的位置;
的位置;
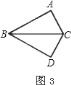
如图![]() ,以
,以![]() 为轴把
为轴把![]() 翻折
翻折![]() ,可以变到
,可以变到![]() 的位置;
的位置;
如图![]() ,以点
,以点![]() 为中心把
为中心把![]() 旋转
旋转![]() ,可以变到
,可以变到![]() 的位置.
的位置.
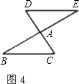
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
回答下列问题:
①在图![]() 中,可以通过平行移动、翻折、旋转中的哪一种方法使
中,可以通过平行移动、翻折、旋转中的哪一种方法使![]() 变到
变到![]() 的位置,
的位置,
答:________.
②指出图![]() 中,线段
中,线段![]() 与
与![]() 之间的关系.
之间的关系.
答:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
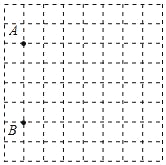
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.
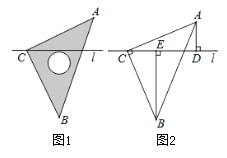
(1)△ACD与△CBE全等吗?说明你的理由.
(2)若AD=2,DE=3.5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(![]() ,0)、B(3
,0)、B(3![]() ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A. 2![]() ﹣2 B. 2
﹣2 B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
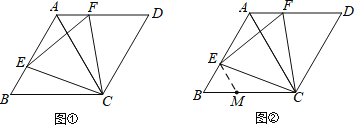
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△OAB的顶点A(6,0),B(0,2),O是坐标原点.将△OAB 绕点O按逆时针旋转90°得到△ODC.
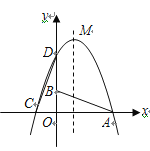
(1)写出C、D两点的坐标;
(2)求过C、D、A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得MA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com