
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
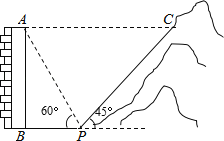
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
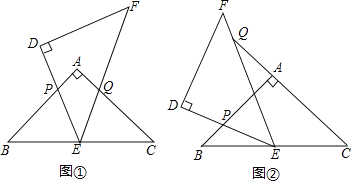
(1)如图①,当点Q在线段AC上,求证:△BPE∽△CEQ;
(2)如图①,当点Q在线段AC上,当AP=4,BP=8时,求P、Q两点间的距离;
(3)如图②,当点Q在线段CA的延长线上,若BP=2a,CQ=9a,求PE:EQ的值,并直接写出△EPQ的面积 (用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞安市新行政区划调整为5镇10街道,市区总人口687498人,将这个总人口数保留两个有效数字并用科学记数法表示,则为( ).
A.6.8×105 B.6.9×105 C.68×104 D.69×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
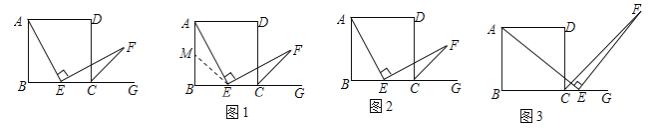
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国某部边防军小分队成一列在野外行军,通讯员在队伍中,数了一下他前后的人数,发现前面人数是后面的两倍,他往前超了6位战士,发现前面的人数和后面的人数一样.
(1)这列队伍一共有多少名战士?
(2)这列队伍要过一座320米的大桥,为安全起见,相邻两个战士保持相同的一定间距,行军速度为5米/秒,从第一位战士刚上桥到全体通过大桥用了100秒时间,请问相邻两个战士间距离为多少米(不考虑战士身材的大小)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com