
【题目】如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
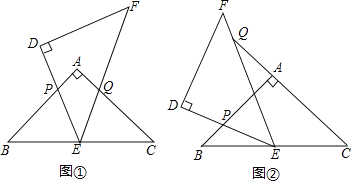
(1)如图①,当点Q在线段AC上,求证:△BPE∽△CEQ;
(2)如图①,当点Q在线段AC上,当AP=4,BP=8时,求P、Q两点间的距离;
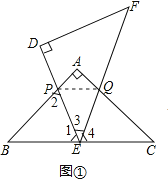
(3)如图②,当点Q在线段CA的延长线上,若BP=2a,CQ=9a,求PE:EQ的值,并直接写出△EPQ的面积 (用含a的代数式表示).
【答案】(1)见解析;(2)PQ=5;(3)![]() a2.
a2.
【解析】
试题分析:(1)由△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,得到∠2=∠4,又由∠B=∠C=45°,即可证得:△BPE∽△CEQ;
(2)连接PQ.根据△BPE∽△CEQ,得到对应边成比例,计算得到CQ=9,AQ=3,由勾股定理可得PQ=5;
(3)根据△BPE∽△CEQ,得到![]() =
=![]() ,求出BE=CE=3
,求出BE=CE=3![]() a,计算即可求出PE:EQ的值,连接PQ,作PH⊥BC于H,PG⊥EF于G,根据等腰直角三角形的性质求出QE、PG,根据三角形的面积公式计算即可.
a,计算即可求出PE:EQ的值,连接PQ,作PH⊥BC于H,PG⊥EF于G,根据等腰直角三角形的性质求出QE、PG,根据三角形的面积公式计算即可.
(1)证明:连接PQ,
∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠1+∠2=135°,
∵△DEF是等腰直角三角形,
∴∠3=45°,
∴∠1+∠4=135°,
∴∠2=∠4,
∵∠B=∠C=45°,
∴△BPE∽△CEQ;
(2)∵AP=4,BP=8,
∴AB=AC=12,
∴BC=12![]() ,
,
∵由(1)知,△BPE∽△CEQ,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴CQ=9,
∴AQAC﹣CQ=3,又AP=4,
∴PQ=5;
(3)∵△BPE∽△CEQ,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,BE=CE=3![]() a,
a,
∴PE:EQ=BP:CE=![]() :3,
:3,
如图②,连接PQ,作PH⊥BC于H,PG⊥EF于G,
∵∠B=45°,BP=2a,
∴PH=BH=![]() a,又BE=3
a,又BE=3![]() a,
a,
∴HE=2![]() a,
a,
∴PE=![]() =
=![]() a,
a,
∴PG=GE=![]() a,
a,
∵PE:EQ=![]() :3,
:3,
∴QE=3![]() a,
a,
∴△EPQ的面积=![]() ×QE×PG=
×QE×PG=![]() a2.
a2.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD,AD∥BC,∠B=90,AD=6,AB=4,BC=9.

(1)求CD的长为.
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣x+m=0有两个不相等的实数根.
(1)求实数m的取值范围;
(2)若方程的两个实数根为x1、x2,且x1+x2+x1x2=m2﹣1,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 过一点有且只有一条直线与已知直线平行
B. 两直线被第三条直线所截,同旁内角互补
C. 不相交的两条直线叫平行线
D. 邻补角的平分线互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
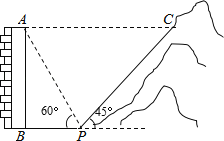
(1)若BP=10m,求居民楼AB的高度;(精确到0.1,![]() ≈1.732)
≈1.732)
(2)若PC=24m,求C、A之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com