
【题目】求证:等腰三角形腰上的高与底边的夹角等于其顶角的一半.
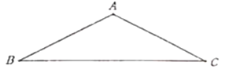
(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言写出“求证”.
已知:在![]() 中,
中,![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
求证:_____________________________________________________.
(2)证明上述命题:
科目:初中数学 来源: 题型:
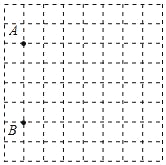
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(![]() ,0)、B(3
,0)、B(3![]() ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A. 2![]() ﹣2 B. 2
﹣2 B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
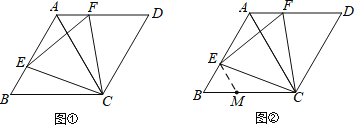
【题目】如图,在菱形ABCD中,∠B= 60°.
(1)如图①.若点E、F分别在边AB、AD上,且BE=AF,求证:△CEF是等边三角形.
(2)小明发现,当点E、F分别在边AB、AD上,且∠CEF=60°时,△CEF也是等边三角形,
并通过画图验证了猜想;小丽通过探索,认为应该以CE= EF为突破口,构造两个全等三角形:小倩受到小丽的启发,尝试在BC上截取BM =BE,并连接ME,如图②,很快就证明了△CEF是等边三角形.请你根据小倩的方法,写出完整的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△OAB的顶点A(6,0),B(0,2),O是坐标原点.将△OAB 绕点O按逆时针旋转90°得到△ODC.
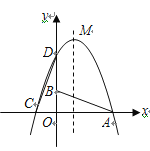
(1)写出C、D两点的坐标;
(2)求过C、D、A三点的抛物线的解析式,并求此抛物线的顶点M的坐标;
(3)在线段AB上是否存在点N使得MA=NM?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )
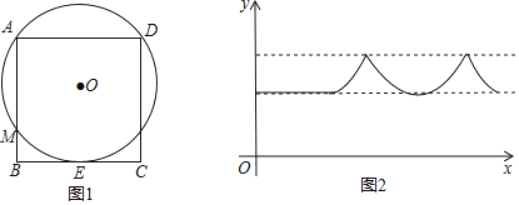
A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为18,阴影部分三角形的面积为8.若AA'=1,则A'D等于 ( )
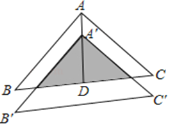
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com