
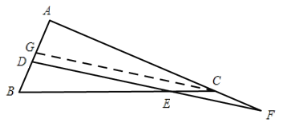
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.

【答案】2
【解析】
过点C作CG∥FD,证得∠F=∠BED=∠CEF,则CF= CE=3,利用AF=AB+BE=5+BE,在![]() 中,根据勾股定理求得BE=10,AC=12,AF=15,利用DE∥CG,求得
中,根据勾股定理求得BE=10,AC=12,AF=15,利用DE∥CG,求得![]() ,利用CG∥FD,求得
,利用CG∥FD,求得![]() ,即可求得
,即可求得![]() 的长.
的长.
如图,过点C作CG∥FD交AB于点G,
∴∠BED=∠BCG,∠ACG=∠F,
∵∠BCA=2∠BED,
∴∠BED=∠BCG=∠ACG,
∴∠F=∠BED=∠CEF,
∴CF= CE=3,
∵AF=AB+BE=5+BE,
∴AC=AF-CF=5+BE-3=2+BE,
在![]() 中,∠BAC=90
中,∠BAC=90![]() ,AB=5,AC= 2+BE,BC=CE+BE=3+BE,
,AB=5,AC= 2+BE,BC=CE+BE=3+BE,
∴![]() ,即
,即![]() ,
,
解得:BE=10,
∴AC=12,AF=15,
∵DE∥CG,
∴![]() ,
,
∴![]() ,
,
∵CG∥FD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:BD=2.
故答案为:2.


科目:初中数学 来源: 题型:
【题目】解答下列各题
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
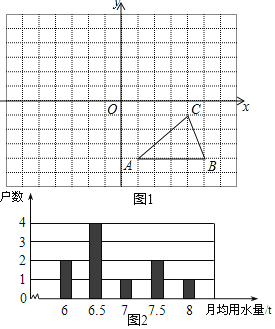
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知卖出的糖果数量x(kg)与售价y(元)的关系如下表:
数量x(kg) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 |
(1)这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
(2)若某顾客付了14.7元,则他购买了多少千克的糖果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为 10cm 的⊙O 中,两条弦 AB,CD 分别位于圆心的异侧,AB∥CD,且![]() ,若 AB=8cm,则 CD 的长为_____cm.
,若 AB=8cm,则 CD 的长为_____cm.
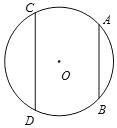
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投入研发费用80万元![]() 万元只计入第一年成本
万元只计入第一年成本![]() ,成功研发出一种产品
,成功研发出一种产品![]() 公司按订单生产
公司按订单生产![]() 产量
产量![]() 销售量
销售量![]() ,第一年该产品正式投产后,生产成本为6元
,第一年该产品正式投产后,生产成本为6元![]() 件
件![]() 此产品年销售量
此产品年销售量![]() 万件
万件![]() 与售价
与售价![]() 元
元![]() 件
件![]() 之间满足函数关系式
之间满足函数关系式![]() .
.
![]() 求这种产品第一年的利润
求这种产品第一年的利润![]() 万元
万元![]() 与售价
与售价![]() 元
元![]() 件
件![]() 满足的函数关系式;
满足的函数关系式;
![]() 该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
该产品第一年的利润为20万元,那么该产品第一年的售价是多少?
![]() 第二年,该公司将第一年的利润20万元
第二年,该公司将第一年的利润20万元![]() 万元只计入第二年成本
万元只计入第二年成本![]() 再次投入研发,使产品的生产成本降为5元
再次投入研发,使产品的生产成本降为5元![]() 件
件![]() 为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件
为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件![]() 请计算该公司第二年的利润
请计算该公司第二年的利润![]() 至少为多少万元.
至少为多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划成立下列学生社团: A.合唱团: B.英语俱乐部: C.动漫创作社; D.文学社:E.航模工作室为了解同学们对上述学生社团的喜爱情况某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调查,根据调查结果绘制了如下尚不完整的统计图.
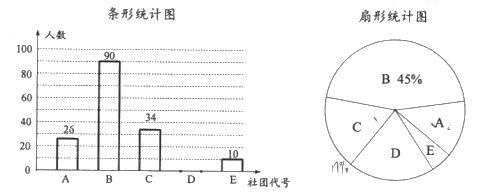
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有多少人;
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为多少;
(3)若该学校共有学生3000人,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:等腰三角形腰上的高与底边的夹角等于其顶角的一半.
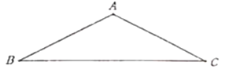
(1)在图中按照下面“已知”的要求,画出符合题意的图形,并根据题设和结论,结合图形,用符号语言写出“求证”.
已知:在![]() 中,
中,![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
求证:_____________________________________________________.
(2)证明上述命题:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com