
【题目】如图,线段AB为⊙O的直径,点C,E在⊙O上,![]() ,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
,CD⊥AB,垂足为点D,连接BE,弦BE与线段CD相交于点F.
(1)求证:CF=BF;
(2)若cos∠ABE![]() ,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.
,在AB的延长线上取一点M,使BM=4,⊙O的半径为6.求证:直线CM是⊙O的切线.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)延长CD交⊙O于G,如图,利用垂径定理得到![]() ,则可证明
,则可证明![]() ,然后根据圆周角定理得∠CBE=∠GCB,从而得到CF=BF ;
,然后根据圆周角定理得∠CBE=∠GCB,从而得到CF=BF ;
(2)连接OC交BE于H,如图,先利用垂径定理得到OC⊥BE ,再在Rt△OBH中利用解直角三角形得到BH![]() ,OH
,OH![]() ,接着证明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根据切线的判定定理得到结论.
,接着证明△OHB∽△OCM得到∠OCM=∠OHB=90°,然后根据切线的判定定理得到结论.
(1)延长CD交⊙O于G,如图,
∵CD⊥AB,∴![]() ,
,
![]() ,∴
,∴![]() ,
,
∴∠CBE=∠GCB,
∴CF=BF;
(2)连接OC交BE于H,如图,
∵![]() ,∴OC⊥BE,
,∴OC⊥BE,
在Rt△OBH中,cos∠OBH![]() ,
,
∴BH![]() ,
,
∴OH![]()
![]() ,
,
∴![]() ,而∠HOB=∠COM,
,而∠HOB=∠COM,
∴△OHB∽△OCM,
∴∠OCM=∠OHB=90°,
∴OC⊥CM,
∴直线CM是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】近几年杭州市推出了“微公交”,“微公交”是国内首创的纯电动汽车租赁服务.它作为一种绿色出行方式,对缓解交通堵塞和停车困难,改善城市大气环境,都可以起到积极作用.据了解某租赁点拥有“微公交”![]() 辆.据统计,当每辆车的年租金为
辆.据统计,当每辆车的年租金为![]() 千元时可全部租出;每辆车的年租金每增加
千元时可全部租出;每辆车的年租金每增加![]() 千元,未租出的车将增加
千元,未租出的车将增加![]() 辆.
辆.
(1)当每辆车的年租金定为![]() 千元时,能租出多少辆?
千元时,能租出多少辆?
(2)当每辆车的年租金增加多少千元时,租赁公司的年收益(不计车辆维护等其他费用)可达到![]() 千元?
千元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)

A. 30.6 B. 32.1 C. 37.9 D. 39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
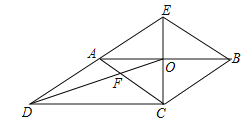
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(120>x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,月销售额为14000元,此月共盈利多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知网格上最小的正方形的边长为1.
(1)分别写出A,B,C三点的坐标;
A_____________;B_____________;C _____________.
(2)作△ABC关于y轴的对称图形△A′B′C′;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
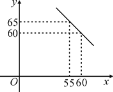
【题目】某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com