
”¾ĢāÄæ”æijĢåÓżÓĆĘ·ÉĢµźŹŌĻśŅ»æī³É±¾ĪŖ50ŌŖµÄÅÅĒņ£¬¹ę¶ØŹŌĻśĘŚ¼äµ„¼Ū²»µĶÓŚ³É±¾¼Ū£¬ĒŅ»ńĄū²»µĆøßÓŚ40%£®¾ŹŌĻś·¢ĻÖ£¬ĻśŹŪĮæy£Øøö£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼äĀś×ćČēĶ¼ĖłŹ¾µÄŅ»“ĪŗÆŹż¹ŲĻµ£®
£Ø1£©ŹŌČ·¶ØyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ČōøĆĢåÓżÓĆĘ·ÉĢµźŹŌĻśµÄÕāæīÅÅĒņĖł»ńµĆµÄĄūČóQŌŖ£¬ŹŌŠ“³öĄūČóQ£ØŌŖ£©ÓėĻśŹŪµ„¼Ūx£ØŌŖ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»µ±ŹŌĻśµ„¼Ū¶ØĪŖ¶ąÉŁŌŖŹ±£¬øĆÉĢµźæÉ»ń×ī“óĄūČó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
£Ø3£©ČōøĆÉĢµźŹŌĻśÕāæīÅÅĒņĖł»ńµĆµÄĄūČó²»µĶÓŚ600ŌŖ£¬ĒėČ·¶ØĻśŹŪµ„¼ŪxµÄȔֵ·¶Ī§£®
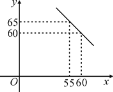
”¾“š°ø”æ£Ø1£© y£½£x£«120£»£Ø2£© Q£½©x2+170x©6000£¬µ±ŹŌĻśµ„¼Ū¶ØĪŖ70ŌŖŹ±£¬øĆÉĢµźæÉ»ń×ī“óĄūČó£¬×ī“óĄūČóŹĒ1000ŌŖ£»£Ø3£©µ„¼ŪĪŖ60”Üx”Ü70µÄÕūŹż£®
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·Ø½«Ķ¼ÖŠµćµÄ×ų±źĒó³öŅ»“ĪŗÆŹż½āĪöŹ½¼“æÉ£»
£Ø2£©øł¾ŻĄūČó£½£ØŹŪ¼Ū©³É±¾£©”ĮĻśŹŪĮæĮŠ³öŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ĮīŗÆŹż¹ŲĻµŹ½Q”Ż600£¬½āµĆxµÄ·¶Ī§£¬ĄūÓĆ”°»ńĄū²»µĆøßÓŚ40%”±ĒóµĆxµÄ×ī“óÖµ£¬µĆ³öĻśŹŪµ„¼ŪxµÄ·¶Ī§£®
£Ø1£©Éčy£½kx+b£¬øł¾ŻĢāŅāµĆ£ŗ
![]()
½āµĆ£ŗk£½©1£¬b£½120£®
ĖłĒóŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½ĪŖy£½©x+120£®
£Ø2£©ĄūČóQÓėĻśŹŪµ„¼ŪxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗQ£½£Øx©50£©£Ø©x+120£©£½©x2+170x©6000£»Q£½©x2+170x©6000£½©£Øx©85£©2+1225£»
”߳ɱ¾ĪŖ50ŌŖµÄÅÅĒņ£¬¹ę¶ØŹŌĻśĘŚ¼äµ„¼Ū²»µĶÓŚ³É±¾¼Ū£¬ĒŅ»ńĄū²»µĆøßÓŚ40%£¬”ą50”Üx”Ü70£¬”ąµ±ŹŌĻśµ„¼Ū¶ØĪŖ70ŌŖŹ±£¬øĆÉĢµźæÉ»ń×ī“óĄūČó£¬×ī“óĄūČóŹĒ1000ŌŖ£®
£Ø3£©ŅĄĢāŅāµĆ£ŗ©x2+170x©6000”Ż600£¬½āµĆ£ŗ60”Üx”Ü110£®
”ß»ńĄū²»µĆøßÓŚ40%£¬”ą×īøß¼ŪøńĪŖ50£Ø1+40%£©£½70£¬¹ŹĻśŹŪµ„¼ŪxµÄȔֵ·¶Ī§ŹĒ60”Üx”Ü70µÄÕūŹż£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ļ߶ĪABĪŖ”ŃOµÄÖ±¾¶£¬µćC£¬EŌŚ”ŃOÉĻ£¬![]() £¬CD”ĶAB£¬“¹×ćĪŖµćD£¬Į¬½ÓBE£¬ĻŅBEÓėĻ߶ĪCDĻą½»ÓŚµćF£®
£¬CD”ĶAB£¬“¹×ćĪŖµćD£¬Į¬½ÓBE£¬ĻŅBEÓėĻ߶ĪCDĻą½»ÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗCF£½BF£»
£Ø2£©Čōcos”ĻABE![]() £¬ŌŚABµÄŃÓ³¤ĻßÉĻČ”Ņ»µćM£¬Ź¹BM£½4£¬”ŃOµÄ°ė¾¶ĪŖ6£®ĒóÖ¤£ŗÖ±ĻßCMŹĒ”ŃOµÄĒŠĻߣ®
£¬ŌŚABµÄŃÓ³¤ĻßÉĻČ”Ņ»µćM£¬Ź¹BM£½4£¬”ŃOµÄ°ė¾¶ĪŖ6£®ĒóÖ¤£ŗÖ±ĻßCMŹĒ”ŃOµÄĒŠĻߣ®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
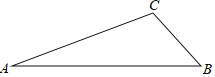
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖ½°åÖŠ£¬AC=4£¬BC=2£¬AB=5£¬PŹĒACÉĻŅ»µć£¬¹żµćPŃŲÖ±Ļß¼ōĻĀŅ»øöÓė”÷ABCĻąĖʵĊ”Čż½ĒŠĪÖ½°å£¬Čē¹ūÓŠ4ÖÖ²»Ķ¬µÄ¼ō·Ø£¬ÄĒĆ“AP³¤µÄȔֵ·¶Ī§ŹĒ__£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ”÷ABCĪŖµČ±ßČż½ĒŠĪ£¬PŹĒÖ±ĻßACÉĻŅ»µć£¬AD”ĶBPÓŚD£¬ŅŌADĪŖ±ß×÷µČ±ß”÷ADE£ØD£¬EŌŚÖ±ĻßACŅģ²ą£©£®
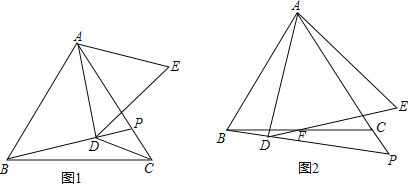
£Ø1£©ČēĶ¼1£¬ČōµćPŌŚ±ßACÉĻ£¬Į¬CD£¬ĒŅ”ĻBDC=150”ć£¬Ōņ![]() = £»£ØÖ±½ÓŠ“½į¹ū£©
= £»£ØÖ±½ÓŠ“½į¹ū£©
£Ø2£©ČēĶ¼2£¬ČōµćPŌŚACŃÓ³¤ĻßÉĻ£¬DE½»BCÓŚFĒóÖ¤£ŗBF=CF£»
£Ø3£©ŌŚĶ¼2ÖŠ£¬Čō”ĻPBC=15”ć£¬AB=![]() £¬ĒėÖ±½ÓŠ“³öCPµÄ³¤ £®
£¬ĒėÖ±½ÓŠ“³öCPµÄ³¤ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬”ŃO¹żÕż·½ŠĪABCDµÄ¶„µćA”¢DĒŅÓė±ßBCĻąĒŠÓŚµćE£¬·Ö±š½»AB”¢DCÓŚµćM”¢N.¶ÆµćPŌŚ”ŃO»ņÕż·½ŠĪABCDµÄ±ßÉĻŅŌĆæĆėŅ»øöµ„Ī»µÄĖŁ¶Č×öĮ¬ŠųŌČĖŁŌĖ¶Æ.ÉčŌĖ¶ÆµÄŹ±¼äĪŖx£¬Ō²ŠÄOÓėPµćµÄ¾ąĄėĪŖy£¬Ķ¼2¼ĒĀ¼ĮĖŅ»¶ĪŹ±¼äĄļyÓėxµÄŗÆŹż¹ŲĻµ£¬ŌŚÕā¶ĪŹ±¼äĄļPµćµÄŌĖ¶ÆĀ·¾¶ĪŖ£Ø £©

A. “ÓDµć³ö·¢£¬ŃŲ»”DA”ś»”AM”śĻ߶ĪBM”śĻ߶ĪBC
B. “ÓBµć³ö·¢£¬ŃŲĻ߶ĪBC”śĻ߶ĪCN”ś»”ND”ś»”DA
C. “ÓAµć³ö·¢£¬ŃŲ»”AM”śĻ߶ĪBM”śĻ߶ĪBC”śĻ߶ĪCN
D. “ÓCµć³ö·¢£¬ŃŲĻ߶ĪCN”ś»”ND”ś»”DA”śĻ߶ĪAB
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
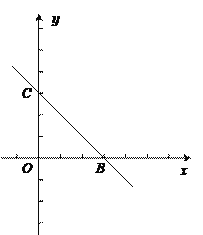
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±ĻßBCÓėÅ×ĪļĻßy=x2+bx+c½»ÓŚµćB£Ø3£¬0£©ŗĶµćC£Ø0£¬3£©£¬Å×ĪļĻßy=x2+bx+c¹żµćB”¢CĒŅÓėxÖįµÄĮķŅ»øö½»µćĪŖA£®
£Ø1£©ĒóÖ±ĻßBC¼°øĆÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ÉčøĆÅ×ĪļĻߵĶ„µćĪŖD£¬Ēó”÷DBCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
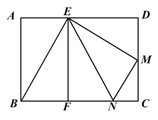
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬µćEŹĒ±ßADÉĻŅ»µć£¬¹żµćE×÷EF”ĶBC£¬“¹×ćĪŖµćF£¬½«”÷BEFČĘ×ŵćEÄꏱÕėŠż×Ŗ£¬Ź¹µćBĀäŌŚ±ßBCÉĻµÄµćN“¦£¬µćFĀäŌŚ±ßDCÉĻµÄµćM“¦£¬ČōµćMĒ”ŗĆŹĒ±ßCDµÄÖŠµć£¬ÄĒĆ“![]() µÄÖµŹĒ£Ø £©
µÄÖµŹĒ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ»ĘŗÓ£¬¼ČŹĒŅ»ĢõŌ“Ō¶Į÷³¤”¢²ØĄ½×³Ą«µÄ×ŌČ»ŗÓ£¬ÓÖŹĒŅ»ĢõŌŠÓżÖŠ»ŖĆń×å²ÓĄĆĪÄĆ÷µÄÄøĒ×ŗÓ£®ŹżŃ§æĪĶāŹµ¼ł»ī¶ÆÖŠ£¬Š”ĮÖŗĶĶ¬Ń§ĆĒŌŚ»ĘŗÓÄĻ°¶Š”Ā·ÉĻµÄA£¬BĮ½µć“¦£¬ÓĆ²ā½ĒŅĒ·Ö±š¶Ō±±°¶µÄ¹Ū¾°Ķ¤D½ųŠŠ²āĮ森ČēĶ¼£¬²āµĆ”ĻDAC=45”ć£¬”ĻDBC=65”ć£®ČōAB=200Ć×£¬Ēó¹Ū¾°Ķ¤Dµ½Š”Ā·ACµÄ¾ąĄėŌ¼ĪŖ¶ąÉŁĆ×£æ£Ø½į¹ū¾«Č·µ½1Ć×£¬²Īæ¼Źż¾Ż£ŗsin65”ć”Ö0.91£¬cos65”ć”Ö0.42£¬tan65”ć”Ö2.14£©


²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
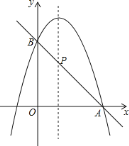
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=©x2+2x+mµÄĶ¼Ļó¹żµćA£Ø3£¬0£©£¬ÓėyÖį½»ÓŚµćB£¬Ö±ĻßABÓėÕāøö¶ž“ĪŗÆŹżĶ¼ĻóµÄ¶Ō³ĘÖį½»ÓŚµćP£¬ĒóµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com