
【题目】已知抛物线y=x2+mx﹣2m﹣4(m>0).
(1)证明:该抛物线与x轴总有两个不同的交点;
(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.
①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;
②若点C关于直线x![]() 的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求
的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)①定点F的坐标为(0,1);②![]() .
.
【解析】
(1)令y=0,再求出判别式,判断即可得出结论;
(2)先求出OA=2,OB=m+2,OC=2(m+2),
①判断出∠OCB=∠OAF,求出tan∠OCB=![]() ,即可求出OF=1,即可得出结论;
,即可求出OF=1,即可得出结论;
②先设出BD=n,再判断出∠DCE=90°,得出DE是⊙P的直径,进而求出BE=2n,DE=![]() n,即可得出结论.
n,即可得出结论.
(1)令y=0,则x2+mx﹣2m﹣4=0,
∴△=m2﹣4[﹣2m﹣4]=m2+8m+16,
∵m>0,
∴△>0,
∴该抛物线与x轴总有两个不同的交点;
(2)令y=0,则x2+mx﹣2m﹣4=0,
∴(x﹣2)[x+(m+2)]=0,
∴x=2或x=﹣(m+2),
∴A(2,0),B(﹣(m+2),0),
∴OA=2,OB=m+2,
令x=0,则y=﹣2(m+2),
∴C(0,﹣2(m+2)),
∴OC=2(m+2),
①通过定点(0,1)理由:如图,
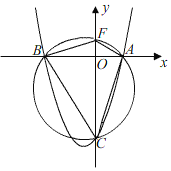
∵点A,B,C在⊙P上,
∴∠OCB=∠OAF,
在Rt△BOC中,tan∠OCB![]() ,
,
在Rt△AOF中,tan∠OAF![]() ,
,
∴OF=1,
∴点F的坐标为(0,1);
②如图1,
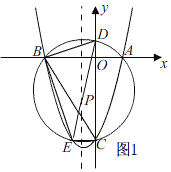
由①知,点F(0,1).
∵D(0,1),
∴点D在⊙P上,
∵点E是点C关于抛物线的对称轴的对称点,
∴∠DCE=90°,
∴DE是⊙P的直径,
∴∠DBE=90°,
∵∠BED=∠OCB,
∴tan∠BED![]() ,
,
设BD=n,在Rt△BDE中,tan∠BED![]() ,
,
∴BE=2n,根据勾股定理得:DE![]() n,
n,
∴l=BD+BE+DE=(3![]() )n,r
)n,r![]() DE
DE![]() n,
n,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在学完二次函数的图像及其性质后,老师让学生们说出![]() 的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是
的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是![]() ”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值,
”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值, ![]() ”……请问这四位同学谁说的结论是错误的( )
”……请问这四位同学谁说的结论是错误的( )
A. 小亮 B. 小丽 C. 小红 D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
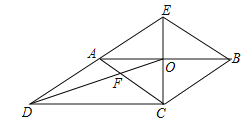
【题目】如图,CE是ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E.连接AC,BE,DO,DO与AC交于点F,则下列结论:
①四边形ACBE是菱形;
②∠ACD=∠BAE;
③AF:BE=2:3;
④S四边形AFOE:S△COD=2:3.
其中正确的结论有_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
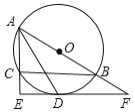
【题目】如图,![]() 是
是![]() ABC的外接圆,AB为直径,∠BAC的平分线交
ABC的外接圆,AB为直径,∠BAC的平分线交![]() 于点D,过点D作DE
于点D,过点D作DE![]() AC分别交AC、AB的延长线于点E、F.
AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是![]() 的切线;
的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留
的长度.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
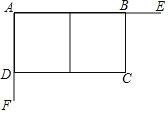
【题目】如图,某工程队在工地互相垂直的两面墙AE、AF处,用180米长的铁栅栏围成一个长方形场地ABCD,中间用同样材料分割成两个长方形.已知墙AE长120米,墙AF长40米,要使长方形ABCD的面积为4000平方米,问BC和CD各取多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com