练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是一座人行天桥引桥部分的示意图，上桥通道AD∥BE，水平平台DE和地面AC平行，立柱BC和地面AC垂直，∠A=37°.已知天桥的高度BC为4.8米，引桥的水平跨度AC为8米，求水平平台DE的长度.（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

    【答案】1.6米.

    【解析】

    试题首先由已知构造直角三角形如图，延长BE交AC于F，由已知BE∥AD，四边形AFED为平行四边形，所以DE=AF，再解直角三角形BCF求得CF即可求得AF．

    试题解析：延长BE交AC于点F

    ∵AD∥BE

    ∴∠BFC=∠A=37°

    又∵BC⊥AC,即∠C=90°

    ∴tan∠BFC

    ∴FC=米

    ∴AF=AC-FC=8-6.4=1.6米

    ∵AD∥BE, DE∥AC

    ∵四边形ADEF是平行四边形

    ∴DE=AF=1.6米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

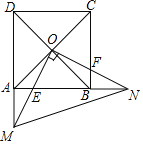
    【题目】如图，正方形ABCD的对角线交于点O，点E、F分别在AB、BC上（AE＜BE），且∠EOF=90°，OE、DA的延长线交于点M，OF、AB的延长线交于点N，连接MN．

    （1）求证：OM=ON．

    （2）若正方形ABCD的边长为4，E为OM的中点，求MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.

    （1）求A、B、C的坐标；

    （2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；

    （3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）.若FG=DQ，求点F的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

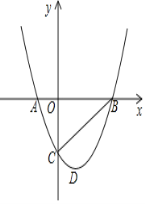
    【题目】如图，平面直角坐标系中，二次函数y=x2﹣2x﹣3的部分图象与x轴交于点A、

    B（A在B的左边），与y轴交于点C，连接BC，D为顶点．

    （1）求∠OBC的度数；

    （2）在x轴下方的抛物线上是否存在一点Q，使△ABQ的面积等于5？如存在，求Q点的坐标，如不存在，说明理由；

    （3）点P是第四象限的抛物线上的一个动点（不与点D重合），过点P作PF⊥x轴交BC于点F，求线段PF长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

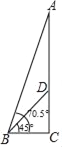
    【题目】位于河南省郑州市的炎黄二帝巨型塑像，是为代表中华民族之创始、之和谐、之统一．塑像由山体CD和头像AD两部分组成．某数学兴趣小组在塑像前50米处的B处测得山体D处的仰角为45°，头像A处的仰角为70.5°，求头像AD的高度．（最后结果精确到0.1米，参考数据：sin70.5°≈0.943，cos70.5°≈0.334，tan70.5°≈2.824）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

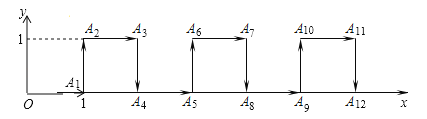
    【题目】在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m．其行走路线如图所示，第1次移动到A1，第2次移动到A2，…，第n次移动到An．则△OA2A2018的面积是（　　）

    A. 504m2 B. m2 C. m2 D. 1009m2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝x2+mx﹣2m﹣4（m＞0）．

    （1）证明：该抛物线与x轴总有两个不同的交点；

    （2）设该抛物线与x轴的两个交点分别为A，B（点A在点B的右侧），与y轴交于点C，A，B，C三点都在⊙P上．

    ①试判断：不论m取任何正数，⊙P是否经过y轴上某个定点？若是，求出该定点的坐标；若不是，说明理由；

    ②若点C关于直线x的对称点为点E，点D（0，1），连接BE，BD，DE，△BDE的周长记为l，⊙P的半径记为r，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

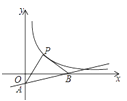
    【题目】如图，直线y=x﹣1与坐标轴交于A，B两点，点P是曲线y=（x＞0）上一点，若△PAB是以∠APB=90°的等腰三角形，则k= _________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着人们生活水平的不断提高，旅游已成为人们的一种生活时尚．为 开发新的旅游项目，我市对某山区进行调查，发现一瀑布．为测量它的高度，测 量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°，测得瀑布底端 B 点的俯角是 10°，AB 与水平面垂直．又在瀑布下的水平面测得 CG=27m， GF=17.6m（注：C、G、F 三点在同一直线上，CF⊥AB 于点 F）．斜坡 CD=20m， 坡角∠ECD=40°．求瀑布 AB 的高度．（参考数据：≈1.73，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin10°≈0.17，cos10°≈0.98，tan10°≈0.18）

    查看答案和解析>>

    同步练习册答案