
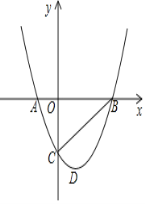
����Ŀ����ͼ��ƽ��ֱ������ϵ�У����κ���y=x2��2x��3�IJ���ͼ����x�ύ�ڵ�A��
B��A��B����ߣ�����y�ύ�ڵ�C������BC��DΪ���㣮
��1������OBC�Ķ�����
��2����x���·������������Ƿ����һ��Q��ʹ��ABQ���������5������ڣ���Q������꣬�粻���ڣ�˵�����ɣ�
��3����P�ǵ��������������ϵ�һ�����㣨�����D�غϣ�������P��PF��x�ύBC�ڵ�F�����߶�PF���ȵ����ֵ��
���𰸡���1����OBC=45�㣻��2����Q������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ������3��PF�����ֵ��
������3��PF�����ֵ��![]() ��
��
��������
��1������������֪�������������OBC�ĸ������㣬��֪��������״���ڽǣ�
��2����Ϊ�������ѹ̶����������Q��AB�ľ���Ϊa�Լ���ABQ���������5�����a��ֵ��Ȼ�������κ����ı���ʽ���������Q�����ꣻ
��3��PF�ij��ȼ�ΪyF-yP����P��F�ĺ�������ͬ�����ֱ�����ý���ʽ��������ú���Ϊ���κ���������ö��κ�������������ֵ���ⷨ���森
��1����y=x2-2x-3=��x-3����x+1����
�൱x=0ʱ��y=-3����y=0ʱ��x=-1��x=3��
���C��������0��-3������B��3��0������A��-1��0����
��OC=3��OB=3��
��OB=OC��
���OBC=��OCB��
�ߡ�BOC=90����
���OBC=��OCB=45����
����OBC=45����
��2����x���·����������ϴ���һ��Q��ʹ��ABQ���������5��
�ߵ�B��3��0������A��-1��0����
��AB=4��
���Q��AB�ľ���Ϊa��
�ߡ�ABQ���������5��
��![]() =5����a=
=5����a=![]() ��
��
�ߵ�Q��x���·���
���Q����������-![]() ��
��
��y=-![]() ����y=x2-2x-3����
����y=x2-2x-3����
-![]() =x2-2x-3��
=x2-2x-3��
��ã�x=![]() ��
��
���Q��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3��
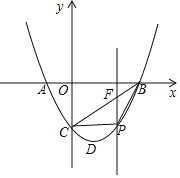
�����C��0��-3���͵�B��3��0����ֱ�߽���ʽΪy=kx+b��
![]() ����
����![]() ��
��
��ֱ��BC�ĺ�������ʽΪy=x-3��
���P��������m��m2-2m-3����
��x=m����y=x-3����y=m-3��
���F��������m��m-3����
��PF=m-3-��m2-2m-3��=-m2+3m=-��m-![]() ��2+
��2+![]() ��
��
�൱m=![]() ʱ��PFȡ�����ֵ����ʱPF=
ʱ��PFȡ�����ֵ����ʱPF=![]() ��
��
��PF�����ֵ��![]() ��
��


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ�г���ɫ���������ͬ��5��С�����к���3��������2����
��1�����ȴӴ���ȡ��x��x��0���������ٴӴ������������1������������������Ϊ�¼�A����AΪ��Ȼ�¼�����x��ֵΪ�� ����
��2�����Ӵ����������2�������ú������1�����û���״ͼ���б���������¼��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���![]() �ڵ�һ���ޣ�
�ڵ�һ���ޣ�![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����һ����������ͼ��պù���
����һ����������ͼ��պù���![]() ��
��

��1���ֱ��������![]() �ķ�����������
�ķ�����������![]() ��
��![]() �����һ�κ����ĺ�������ʽ��
�����һ�κ����ĺ�������ʽ��
��2��ֱ��![]() �ᣬ����
�ᣬ����![]() ���������ÿ��
���������ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() ���������˶���������������ͼ���ڵ�
���������˶���������������ͼ���ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����ֱ��
����ֱ��![]() �˶���������
�˶���������![]() ʱ��ֹͣ�˶������˶�ʱ��Ϊ
ʱ��ֹͣ�˶������˶�ʱ��Ϊ![]() ���룩��
���룩��
���ʣ��Ƿ����![]() ��ֵ��ʹ�ı���
��ֵ��ʹ�ı���![]() Ϊƽ���ı��Σ������ڣ����
Ϊƽ���ı��Σ������ڣ����![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
����ֱ��![]() ��
��![]() �������ͬʱ����һ����
�������ͬʱ����һ����![]() �ӵ�
�ӵ�![]() ������������
������������![]() ������ÿ��
������ÿ��![]() ����λ���ȵ��ٶ��˶����Ƿ����
����λ���ȵ��ٶ��˶����Ƿ����![]() ��ֵ��ʹ�Ե�
��ֵ��ʹ�Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊƽ���ı��Σ������ڣ����
Ϊ������ı���Ϊƽ���ı��Σ������ڣ����![]() ��ֵ������һ��̽����ʱ���ı����Ƿ�Ϊ�����ƽ���ı��Σ��������ڣ�˵�����ɣ�
��ֵ������һ��̽����ʱ���ı����Ƿ�Ϊ�����ƽ���ı��Σ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�Ա�У��2017��500��ѧ�����п��μ��������Բ���������е��飬��������1000��Ů��800�ײ��Գɼ����������Ƴɲ�������ͳ��ͼ����ͼ�٣�ͼ�ڣ��������ͳ��ͼ�ṩ����Ϣ���ش��������⣺
��1����У��ҵ���������� �ˣ�����ͳ��ͼ��a= ��

��2����ȫ����ͳ��ͼ��
��3����500��ѧ���������ȡһ��ѧ��������ѧ������ɼ���8�ּ�8�����µĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+2x��1��
��1��д�����Ķ������ꣻ
��2����xȡ��ֵʱ��y��x�����������
��3����xȡ��ֵʱy��ֵ����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
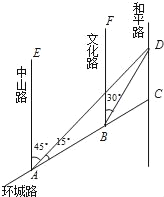
����Ŀ����ͼ��AC��ij�л���·��һ�Σ�AE��BF��CD�����ϱ�����Ľֵ������뻷��·AC�Ľ���·�ڷֱ���A��B��C����������������Dλ�ڵ�A�ı�ƫ��45������B�ı�ƫ��30�������ϣ�AB=2km����DAC=15�㣮
��1����B��D֮��ľ��룻
��2����C��D֮��ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������������Ų��ֵ�ʾ��ͼ������ͨ��AD��BE��ˮƽƽ̨DE�͵���ACƽ�У�����BC�͵���AC��ֱ����A=37��.��֪���ŵĸ߶�BCΪ4.8�������ŵ�ˮƽ���ACΪ8������ˮƽƽ̨DE�ij���.���ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��Ϊ�˽��������±仯�������¼�˽����·�����![]() ���������£���λ��������
���������£���λ��������![]() .�����������ݣ����н��۲���ȷ���ǣ� ��
.�����������ݣ����н��۲���ȷ���ǣ� ��
A��ƽ������![]() B����λ����
B�������![]() C.������
C.������![]() D��������
D��������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵĸߣ�AE��BC���ϵ����ߣ���C=45����sinB=![]() ��AD=1��
��AD=1��
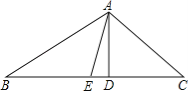
��1����BC�ij���
��2����tan��DAE��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com