
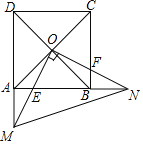
【题目】如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.
(1)求证:OM=ON.
(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.
【答案】(1)见解析;(2)MN =2![]() .
.
【解析】
(1)证△OAM≌△OBN即可得;
(2)作OH⊥AD,由正方形的边长为4且E为OM的中点知OH=HA=2,HM=4,再根据勾股定理得OM=2![]() ,由直角三角形性质知MN=
,由直角三角形性质知MN=![]() OM=2
OM=2![]() .
.
(1)∵四边形ABCD是正方形,
∴OA=OB,∠DAO=45°,∠OBA=45°,
∴∠OAM=∠OBN=135°,
∵∠EOF=90°,∠AOB=90°,
∴∠AOM=∠BON,
∴△OAM≌△OBN(ASA),
∴OM=ON;
(2)如图,过点O作OH⊥AD于点H,

∵正方形的边长为4,
∴OH=HA=2,
∵E为OM的中点,
∴HM=4,
则OM=![]() =2
=2![]() ,
,
∴MN=![]() OM=2
OM=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直径为 10cm 的⊙O 中,两条弦 AB,CD 分别位于圆心的异侧,AB∥CD,且![]() ,若 AB=8cm,则 CD 的长为_____cm.
,若 AB=8cm,则 CD 的长为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
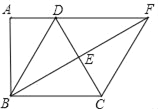
【题目】如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于E交AD的延长线于F,DC=2AD,AB=BE.
(1)求证:AD=DE.
(2)求证:四边形BCFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个,黑球2个.
(1)若先从袋中取出x(x>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,若A为必然事件,则x的值为 ;
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用画树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
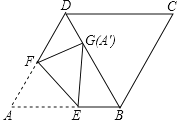
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学完二次函数的图像及其性质后,老师让学生们说出![]() 的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是
的图像的一些性质,小亮说:“此函数图像开口向上,且对称轴是![]() ”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值,
”;小丽说:“此函数肯定与x轴有两个交点”;小红说:“此函数与y轴的交点坐标为(0,-3)”;小强说:“此函数有最小值, ![]() ”……请问这四位同学谁说的结论是错误的( )
”……请问这四位同学谁说的结论是错误的( )
A. 小亮 B. 小丽 C. 小红 D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,有一反比例函数图象刚好过点
,有一反比例函数图象刚好过点![]() .
.

(1)分别求出过点![]() 的反比例函数和过
的反比例函数和过![]() ,
,![]() 两点的一次函数的函数表达式;
两点的一次函数的函数表达式;
(2)直线![]() 轴,并从
轴,并从![]() 轴出发,以每秒
轴出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 轴正方向运动,交反比例函数图象于点
轴正方向运动,交反比例函数图象于点![]() ,交
,交![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当直线
,当直线![]() 运动到经过点
运动到经过点![]() 时,停止运动.设运动时间为
时,停止运动.设运动时间为![]() (秒).
(秒).
①问:是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②若直线![]() 从
从![]() 轴出发的同时,有一动点
轴出发的同时,有一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度运动.是否存在
个单位长度的速度运动.是否存在![]() 的值,使以点
的值,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com