
【题目】随着人们生活水平的不断提高,旅游已成为人们的一种生活时尚.为 开发新的旅游项目,我市对某山区进行调查,发现一瀑布.为测量它的高度,测 量人员在瀑布的对面山上 D 点处测得瀑布顶端 A 点的仰角是 30°,测得瀑布底端 B 点的俯角是 10°,AB 与水平面垂直.又在瀑布下的水平面测得 CG=27m, GF=17.6m(注:C、G、F 三点在同一直线上,CF⊥AB 于点 F).斜坡 CD=20m, 坡角∠ECD=40°.求瀑布 AB 的高度.(参考数据:![]() ≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)
≈1.73,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin10°≈0.17,cos10°≈0.98,tan10°≈0.18)

【答案】瀑布 AB 的高度约为 45.4 米.
【解析】
过点 D 作 DM⊥CE,交 CE 于点 M,作 DN⊥AB,交 AB 于点 N,在 Rt△ CMD 中,通过解直角三角形可求出 CM 的长度,进而可得出 MF、DN 的长度, 再在 Rt△BDN、Rt△ADN 中,利用解直角三角形求出 BN、AN 的长度,结合 AB=AN+BN 即可求出瀑布 AB 的高度.
如图,过点 D 作 DM⊥CE,交 CE 于点 M,作 DN⊥AB,交 AB 于点 N,

在 Rt△CMD 中,CD=20m,∠DCM=40°,∠CMD=90°,
∴CM=CDcos40°≈15.4m,DM=CDsin40°≈12.8m,
∴DN=MF=CM+CG+GF=60m,
在 Rt△BDN 中,∠BDN=10°,∠BND=90°,DN=60m,
∴BN=DNtan10°≈10.8m,
在 Rt△ADN 中,∠ADN=30°,∠AND=90°,DN=60m,
∴AN=DNtan30°≈34.6m,
∴AB=AN+BN=45.4m,
答:瀑布 AB 的高度约为 45.4 米.


科目:初中数学 来源: 题型:
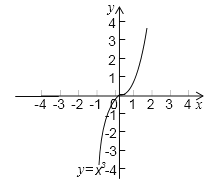
【题目】利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
(2)已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴正半轴上,边
轴正半轴上,边![]() ,
,![]() (
(![]() )的长分别是方程
)的长分别是方程![]() 的两个根,
的两个根,![]() 是边
是边![]() 上的一动点(不与A、B重合).
上的一动点(不与A、B重合).
(1)填空:AB= ,OA= .
(2)若动点D满足△BOC与△AOD相似,求直线![]() 的解析式.
的解析式.
(3)若动点D满足![]() ,且点
,且点![]() 为射线
为射线![]() 上的一个动点,当△PAD是等腰三角形时,直接写出点
上的一个动点,当△PAD是等腰三角形时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型 | B型 | |
价格(万元/台) | m | n |
运载量(吨/车) | 20 | 30 |
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景阅读:
意大利著名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为裴波那契数列.
实践操作:
(1)写出裴波那契数列的前10个数;
(2)裴波那契数列的前2017个数中,有多少个奇数?
(3)现以这组数的各个数作为正方形的边长构造如图1的正方形系列:再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④、⑤……


(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号 | ① | ② | ③ | ④ | ⑤ | …… |
周长 | 6 | 10 | …… |
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形的面积和周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000![]() ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com