
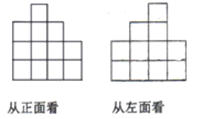
【题目】在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递如图所示,则这正方体快递件最多有_____件.
【答案】39
【解析】
由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得第3层最多正方体的个数为:3×2=6;由主视图和左视图可得第4层最多正方体的个数为:1;相加可得所求.
由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,
最底层几何体最多正方体的个数为:4×4=16,
由主视图和左视图可得第二层最多正方体的个数为:4×4=16;
由主视图和左视图可得第3层最多正方体的个数为:3×2=6;
由主视图和左视图可得第4层最多正方体的个数为:1;
16+16+6+1=39(件).
故这正方体快递件最多有39件.
故答案为:39.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
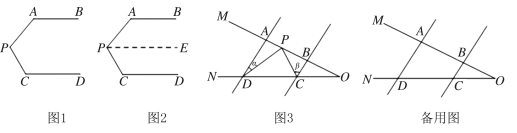
【题目】问题情景:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
(1)数学活动小组经过讨论形成下列推理,请你补全推理依据.
如图2,过点P作PE∥AB,
∵PE∥AB(作图知)
又∵AB∥CD,
∴PE∥CD.( )
∴∠A+∠APE=180°.
∠C+∠CPE=180°.( )
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°
∴∠APC=∠APE+∠CPE=110°.
问题迁移:
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=α,∠BCP=β,求∠CPD与α、β之间有何数量关系?请说明理由.
问题解决:
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与α、β之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
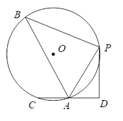
【题目】如图,在⊙O中,B,P,A,C是圆上的点,![]() , PD⊥CD,CD交⊙O于A,若AC=AD,PD =
, PD⊥CD,CD交⊙O于A,若AC=AD,PD = ![]() ,sin∠PAD =
,sin∠PAD = ![]() ,则△PAB的面积为_______.
,则△PAB的面积为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法感悟:
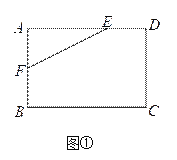
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
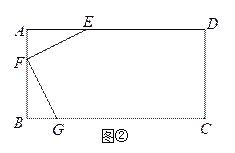
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某种产品展开图,高为3cm.
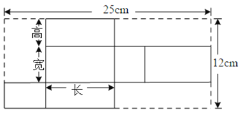
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
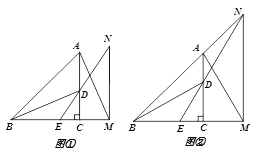
(2)如图①,若点E是BM的中点,求证:MN=AM;
(3)如图②,若点N落在BA的延长线上,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM、ON分别为∠AOC、∠AOB的平分线.
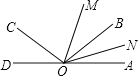
(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=55°,试求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com