
����Ŀ����������
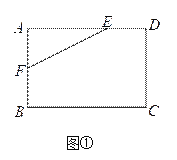
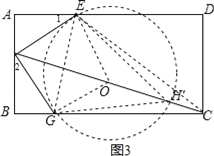
��1����ͼ�٣��ھ���ABCD�У�AB=4��AD=6��AE=4��AF=2���Ƿ��ڱ�BC��CD�Ϸֱ���ڵ�G��H��ʹ���ı���EFGH���ܳ���С�������ڣ�������ܳ�����Сֵ���������ڣ���˵�����ɣ�
��������
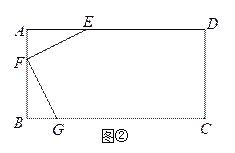
��2����ͼ�ڣ���һ���ΰ��ABCD��AB=3�ף�AD=6�ף�����Ӵ˰���вó�һ����������ܴ���ı���EFGH������ʹ��EFG=90����EF=FG=![]() �ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
�ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1�����ڵ��ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2�������õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() )
)
������������: ��1����E����CD�ĶԳƵ�E�䣬��F����BC�ĶԳƵ�F�䣬����E��F�䣬�õ���ʱ�ı���EFGH���ܳ���С��������ԳƵ����ʵõ�BF�䣽BF��AF��2��DE�䣽DE��2����A��90�㣬���ǵõ�AF�䣽6��AE�䣽8�����E��F�䣽10��EF��2![]() ���ɵõ����ۣ�
���ɵõ����ۣ�
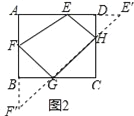
��2��������ǵ����ʵõ�1����2���Ƴ���AEF�ա�BGF������ȫ�������ε����ʵõ�AF��BG��AE��BF����AF��x����AE��BF��3x���ݹ��ɶ����з��̵õ�AF��BG��1��BF��AE��2������EFG����EG�ĶԳơ�EOG�����ı���EFGO�������Σ���EOG��90�㣬��OΪԲ�ģ���EGΪ�뾶����O�����EHG��45��ĵ�H�ڡ�O�ϣ�����FO�����ӳ�����O��H�䣬��H����EG�Ĵ�ֱƽ�����ϣ�����EH��GH�䣬���EH��G��45�㣬���ǵõ��ı���EFGH���Ƿ�����������������ݾ��ε������ʽ���ɵõ����ۣ�
���:
�⣺��1�����ڣ����ɣ���E����CD�ĶԳƵ�E����
��F����BC�ĶԳƵ�F����
����E��F������BC��G����CD��H������FG��EH��
��F��G=FG��E��H=EH�����ʱ�ı���EFGH���ܳ���С��
������ã�BF��=BF=AF=2��DE��=DE=2����A=90����
��AF��=6��AE��=8��
��E��F��=10��EF=2![]() ��
��
���ı���EFGH���ܳ�����Сֵ=EF+FG+GH+HE=EF+E��F��=2![]() +10��
+10��
���ڱ�BC��CD�Ϸֱ���ڵ�G��H��
ʹ���ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2���ܲõã�
���ɣ���EF=FG=![]() ����A=��B=90������1+��AFE=��2+AFE=90����
����A=��B=90������1+��AFE=��2+AFE=90����
���1=��2��
����AEF����BGF�� 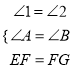 ��
��
���AEF�ա�BGF��
��AF=BG��AE=BF��
��AF=x����AE=BF=3��x��
��x2+��3��x��2=��![]() ��2��
��2��
��ã�x=1��x=2���������⣬��ȥ����
��AF=BG=1��BF=AE=2��
��DE=4��CG=5��
����EG������EFG����EG�ĶԳ���EOG��
���ı���EFGO�������Σ���EOG=90����
��OΪԲ�ģ���EGΪ�뾶����O��
���EHG=45���ĵ��ڡ�O�ϣ�
����FO�����ӳ�����O��H������H����EG�Ĵ�ֱƽ�����ϣ�
����EH��GH�������EH��G=45����
��ʱ���ı���EFGH����Ҫ��õ÷���Ҫ���������ģ�
��C���߶�EG�Ĵ�ֱƽ�����裬
���F��O��H����C��һ��ֱ���ϣ�
��EG=![]() ��
��
��OF=EG=![]() ��
��
��CF=2![]() ��
��
��OC=![]() ��
��
��OH��=OE=FG=![]() ��
��
��OH����OC��
���H���ھ���ABCD���ڲ���
������ھ���ABCD�У��õ÷�����������������ı���EFGH��������
������������=![]() EGFH��=
EGFH��=![]() ��
��![]() ����
����![]() +
+![]() ��=5+
��=5+![]() ��
��
�൱���õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() ).
).

�㾦: ���⿼����ȫ�������ε��ж������ʣ����ε����ʣ����ɶ�������ԳƵ����ʣ����������⣬���յ��������������öԳƵ����ʽ�������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ����ѧҵ�������ػ�����Ӱ��ѧ���Դ�ѧϰ��̬�ȣ�Ϊ�����н������ŶԲ���ѧУ�İ��꼶ѧ���Դ�ѧϰ��̬�Ƚ�����һ�γ������飨��ѧϰ̬�ȷ�Ϊ�����㼶��A������ѧϰ�ܸ���Ȥ��B������ѧϰ�ϸ���Ȥ��C������ѧϰ������Ȥ�����������������Ƴ�ͼ����ͼ����ͳ��ͼ�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������� ��ѧ����
��2����ͼ������������
��3�����ͼ����C����ռ��Բ�ĽǵĶ�����
��4�����ݳ���������������������н�8000�����꼶ѧ���д�Լ�ж�����ѧ��ѧϰ̬�ȴ�꣨������A����B������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У��������ĶԳ�ͼ��������Գ�ͼ�ε��ǣ� ��

A. ��A�� B. ��B�� C. ��C�� D. ��D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
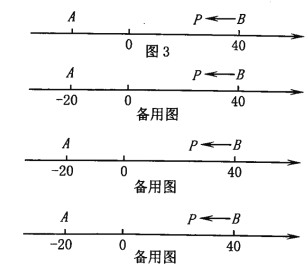
����Ŀ�����Ķ����⣩��A��B��CΪ���������㣬����C��A�ľ���CA�ǵ�C��B�ľ���CB��2�������ǾͳƵ�C�ǣ�A��B���ĺõ�.���磬��ͼ1����A��ʾ����Ϊ��1����B��ʾ����Ϊ2.��ʾ1�ĵ�C����A�ľ���CA��2������B�ľ���CB��1����ô��C�ǣ�A��B���ĺõ㣻���磬��ʾ0�ĵ�D����A�ľ���DA��1������B�ľ���DB��2����ô��D�Ͳ��ǣ�A��B)�ĺõ㣬����D�ǣ�B��A)�ĺõ�.
��֪ʶ���ã�����1)��ͼ1����ʾ��______��_______�ĵ��ǣ�A��B���ĺõ㣻

��2)��ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ4.

�ٱ�ʾ��______�ĵ��ǣ�M��N)�ĺõ㣻
�ڱ�ʾ��______�ĵ��ǣ�N��M)�ĺõ㣻
(3)��ͼ3��A��BΪ���������㣬��A����ʾ����Ϊ��20����B����ʾ����Ϊ40.����һֻ��������P�ӵ�B��������2����λÿ����ٶ������˶�.��tΪ��ֵʱ��P��A��B��ǡ��һ����Ϊ��������ĺõ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶ѧ��С����Сǿ��С�쵽ij���вμ������ʵ������ڻ�����Dz�����ij��ˮ�������۹�������֪��ˮ���Ľ���Ϊ8Ԫ/ǧ�ˣ������������ڻ������ĶԻ���
С���������10Ԫ/ǧ�˵ļ۸����ۣ���ôÿ����۳�300ǧ�ˣ�
Сǿ�����ÿǧ�˵�����Ϊ3Ԫ����ôÿ����۳�250ǧ�ˣ�
С�죺�����13Ԫ/ǧ�˵ļ۸����ۣ���ôÿ��ɻ�ȡ����750Ԫ��
������=�����ۼ�-���ۣ�![]() ��������
��������
��1����������ǵĶԻ���д�±���
���۵���x��Ԫ/kg�� | 10 | 11 | 13 |
������y��kg�� |
��2��������ݱ����е���Ϣ�ж�ÿ���������y��ǧ�ˣ������۵���x��Ԫ��֮����������ĺ�����ϵ������y��ǧ�ˣ���x��Ԫ����x��0���ĺ�����ϵʽ��
��3����ó�����������ˮ��ÿ���ȡ������ΪWԪ����W��x�ĺ�����ϵʽ�������۵���Ϊ��ֵʱ��ÿ��ɻ�õ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪֱ����AB=4��C��DΪԲ���������㣬NΪCD�е㣬CM��AB��M����C��D��Բ���˶�ʱ���֡�CMN=30������CD�ij����� ��
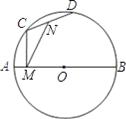
A. ��C��D���˶�λ�ö��仯�������ֵΪ4 B. ��C��D���˶�λ�ö��仯������СֵΪ2
C. ��C��D���˶�λ�ó��ȱ��ֲ��䣬����2 D. ��C��D���˶�λ�ö��仯��û����ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͼ��ݼƻ�ѡ���ס�������ͼ��.��ͼ��ÿ���۸�����ͼ��ÿ���۸��2.5���������900Ԫ����ͼ�飬�������ͼ��ȵ���������ͼ��Ҫ��18��.
��1���ס�������ͼ��ÿ���۸�ֱ�Ϊ����Ԫ��
��2�������ͼ��ݼƻ�������ͼ��ı����ȹ����ͼ�鱾����2����8���������ڹ���ס�������ͼ����ܷ��ò�����1725Ԫ����ô��ͼ��������Թ�����ٱ���ͼ�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬�����Ժ����ר�����ֻᣬ����Ʊÿ��20Ԫ��ѧ��Ʊÿ��5Ԫ��Ϊ���������ʦ���������ֻᣬ��Ժ�ƶ��������Żݷ�����
����һ������һ�ų���Ʊ����һ��ѧ��Ʊ��
������������Ʊ��ѧ��Ʊ�������.
��У����4����ʦ����������������4�ˣ�ѧ�������ֻ�.
��1����ѧ������Ϊ![]() ���ˣ��������ܽ��Ϊ
���ˣ��������ܽ��Ϊ![]() ��Ԫ������ֱ�ȷ�������Żݷ�����
��Ԫ������ֱ�ȷ�������Żݷ�����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������ϲμ������ֻ��ѧ������������˵��������Ʊ�����٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ��������ֽƬABO������ƽ��ֱ������ϵ������A��![]() ��0������B��0��1������O��0��0����P�DZ�AB�ϵ�һ������P�����A��B�غ���������OP�۵���ֽƬ���õ�A�Ķ�Ӧ��A'������BPA'=30��ʱ����P������Ϊ______��
��0������B��0��1������O��0��0����P�DZ�AB�ϵ�һ������P�����A��B�غ���������OP�۵���ֽƬ���õ�A�Ķ�Ӧ��A'������BPA'=30��ʱ����P������Ϊ______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com