
【题目】将一个直角三角形纸片ABO放置在平面直角坐标系中,点A(![]() ,0),点B(0,1),点O(0,0).P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A',当∠BPA'=30°时,点P的坐标为______.
,0),点B(0,1),点O(0,0).P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A',当∠BPA'=30°时,点P的坐标为______.
【答案】(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )
)
【解析】分析:由点A和B的坐标得出OA=![]() ,OB=1,由折叠的性质得:OA'=OA=
,OB=1,由折叠的性质得:OA'=OA=![]() ,由勾股定理求出A'B=
,由勾股定理求出A'B=![]() ,即可得出点A'的坐标为(
,即可得出点A'的坐标为(![]() ,1);由勾股定理求出AB=2,证出OB=OP=BP,得出△BOP是等边三角形,得出∠BOP=∠BPO=60°,求出∠OPA=120°,由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,证出OB∥PA',得出四边形OPA'B是平行四边形,即可得出A'B=OP=1;分两种情况:①点A'在y轴上,由SSS证明△OPA'≌△OPA,得出∠A'OP=∠AOP=
,1);由勾股定理求出AB=2,证出OB=OP=BP,得出△BOP是等边三角形,得出∠BOP=∠BPO=60°,求出∠OPA=120°,由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,证出OB∥PA',得出四边形OPA'B是平行四边形,即可得出A'B=OP=1;分两种情况:①点A'在y轴上,由SSS证明△OPA'≌△OPA,得出∠A'OP=∠AOP=![]() ∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=-
∠AOB=45°,得出点P在∠AOB的平分线上,由待定系数法求出直线AB的解析式为y=-![]() x+1,即可得出点P的坐标;②由折叠的性质得:∠A'=∠A=30°,OA'=OA,作出四边形OAPA'是菱形,得出PA=OA=
x+1,即可得出点P的坐标;②由折叠的性质得:∠A'=∠A=30°,OA'=OA,作出四边形OAPA'是菱形,得出PA=OA=![]() ,作PM⊥OA于M,由直角三角形的性质求出PM=
,作PM⊥OA于M,由直角三角形的性质求出PM=![]() PA=
PA=![]() ,把y=
,把y=![]() 代入y=-
代入y=-![]() x+1求出点P的纵坐标即可.
x+1求出点P的纵坐标即可.
详解:∵点A(![]() ,0),点B(0,1),
,0),点B(0,1),
∴OA=![]() ,OB=1,
,OB=1,
由折叠的性质得:OA'=OA=![]() ,
,
∵A'B⊥OB,
∴∠A'BO=90°,
在Rt△A'OB中,A'B=![]() =
=![]() ,
,
∴点A'的坐标为(![]() ,1);
,1);
(2)在Rt△ABO中,OA=![]() ,OB=1,
,OB=1,
∴AB=![]() =2,
=2,
∵P是AB的中点,
∴AP=BP=1,OP=![]() AB=1,
AB=1,
∴OB=OP=BP
∴△BOP是等边三角形,
∴∠BOP=∠BPO=60°,
∴∠OPA=180°-∠BPO=120°,
由折叠的性质得:∠OPA'=∠OPA=120°,PA'=PA=1,
∴∠BOP+∠OPA'=180°,
∴OB∥PA',
又∵OB=PA'=1,
∴四边形OPA'B是平行四边形,
∴A'B=OP=1
设P(x,y),分两种情况:
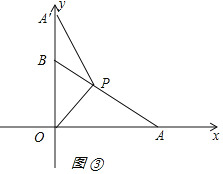
①如图③所示:点A'在y轴上,
在△OPA'和△OPA中,
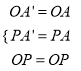 ,
,
∴△OPA'≌△OPA(SSS),
∴∠A'OP=∠AOP=![]() ∠AOB=45°,
∠AOB=45°,
∴点P在∠AOB的平分线上,
设直线AB的解析式为y=kx+b,
把点A(![]() ,0)A(3,0),点B(0,1)代入得:
,0)A(3,0),点B(0,1)代入得:
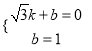 ,
,
解得: 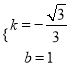 ,
,
∴直线AB的解析式为y=-![]() x+1,
x+1,
∵P(x,y),
∴x=-![]() x+1,
x+1,
解得:x=![]() ,
,
∴P(![]() ,
, ![]() );
);
②如图④所示:
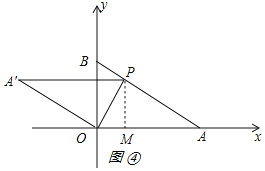
由折叠的性质得:∠A'=∠A=30°,OA'=OA,
∵∠BPA'=30°,
∴∠A'=∠A=∠BPA',
∴OA'∥AP,PA'∥OA,
∴四边形OAPA'是菱形,
∴PA=OA=![]() ,作PM⊥OA于M,如图④所示:
,作PM⊥OA于M,如图④所示:
∵∠A=30°,
∴PM=![]() PA=
PA=![]() ,
,
把y=![]() 代入y=-
代入y=-![]() x+1得:
x+1得: ![]() =-
=-![]() +1,
+1,
解得:x=![]() ,
,
∴P(![]() ,
, ![]() );
);
综上所述:当∠BPA'=30°时,点P的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
点睛:
本题是几何变换综合题目,考查了折叠的性质、坐标与图形性质、勾股定理、平行四边形的判定与性质、全等三角形的判定与性质、角平分线的性质、直角三角形的性质、待定系数法求直线的解析式、菱形的判定与性质等知识;本题综合性强,难度较大.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】方法感悟:
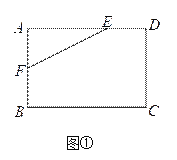
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
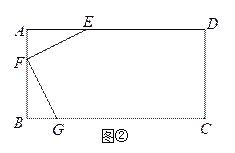
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
(1)求一次函数的解析式.
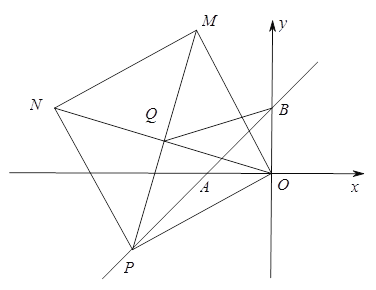
(2)如图,点C与点B关于x轴对称,点D在线段OA上,连结BD,把线段BD顺时针方向旋转90°得到线段DE,作直线CE交x轴于点F,求![]() 的值.
的值.
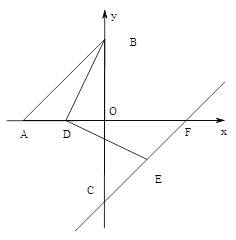
(3)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并回答问题
观察:有理数-2和-4在数轴上对应的两点之间的距离是![]() ,有理数1和-3在数轴上对应的两点之间的距离是
,有理数1和-3在数轴上对应的两点之间的距离是![]()

归纳:有理数a、b在数轴上对应的两点A.B之间的距离是![]() ,反之,
,反之,![]() 表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义
表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义
应用:
(1)如果表示-1的点A和表示x点B之间的距离是2,那么x为________;
(2)方程![]() 的解为________;
的解为________;
(3)小松同学在解方程![]() 时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当
时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当![]() 时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出
时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出![]() ;同理,若x的对应点在-2的左边,可得
;同理,若x的对应点在-2的左边,可得![]() ;故原方程的解是
;故原方程的解是![]() 或
或![]() ;参考小松的解答过程,求方程
;参考小松的解答过程,求方程![]() 的解.
的解.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
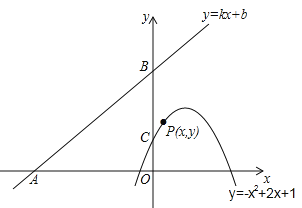
A. 1.4 B. 2.5 C. 2.8 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
(1)这次抽查了四个品牌的饮料共 瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约20万瓶,请你估计这四个品牌的不合格饮料有多少瓶?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
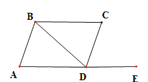
A.∠C=∠CDEB.∠ABD=∠CBDC.∠ABD=∠CDBD.∠C+∠ADC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为四家超市,其中超市D距A,B,C三家超市的路程分别为25km,10km,5km.现计划在A,D之间的道路上建一个配货中心P,为避免交通拥堵,配货中心与超市之间的距离不少于2km.假设一辆货车每天从P出发为这四家超市送货各1次,由于货车每次仅能给一家超市送货,因此每次送货后均要返回配货中心P,重新装货后再前往其他超市.设P到A的路程为xkm,这辆货车每天行驶的路程为ykm.
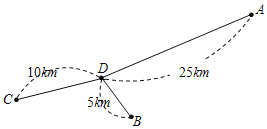
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)直接写出配货中心P建在什么位置,这辆货车每天行驶的路程最短?最短路程是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com