
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
【答案】(1)P(两次抽得纸牌均为红桃) =![]() ;(2)甲选择A方案胜率更高,理由见解析.
;(2)甲选择A方案胜率更高,理由见解析.
【解析】分析: (1)首先根据题意列出表格,然后由表格即可求得所有等可能的结果;
(2)首先求得A方案与B方案中甲胜的概率,比较大小,即可确定甲选择哪种方案胜率更高.
详解:
解:(1)树状图:
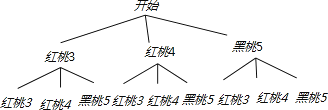
列表:
红桃3 | 红桃4 | 黑桃5 | |
红桃3 | (红3,红3) | (红3,红4) | (红3,黑5) |
红桃4 | (红4,红3) | (红4,红4) | (红4,黑5) |
黑桃5 | (黑5,红3) | (黑5,红4) | (黑5,黑5) |
∴一共有9种等可能的结果,其中符合要求的共4种,
∴P(两次抽得纸牌均为红桃)= ![]() .
.
(2)∵两次抽得相同花色的有5种,两次抽得数字和为奇数有4种,
A方案:P(甲胜)=![]() ,
,
B方案:P(甲胜)=![]() ,
,
∴甲选择A方案胜率更高.
点睛: 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,动点P从O点出发沿OM方向以每秒1cm的速度匀速运动;动点Q从点C出发,在线段CO上向点O匀速运动(点Q运动到点O时,立即停止运动),点P,Q同时出发.
(1)当点P与点Q都同时运动到线段AB的中点时,求点Q的运动速度;
(2)若点Q运动速度为每秒3cm时,经过多少时间P,Q两点相距70cm;
(3)当PA=2PB时,点Q运动的位置恰好是线段AB的三等分,求点Q的速度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
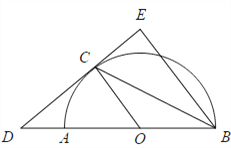
【题目】如图,已知![]() 是
是![]() 的直径,CD与
的直径,CD与![]() 相切于C,
相切于C, ![]() .
.
(1)求证:BC 是![]() 的平分线.
的平分线.
(2)若DC=8, ![]() 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
【答案】(1)证明见解析;(2)4.8
【解析】分析:(1)由![]() ,推出
,推出![]() ,由
,由![]() ,推出
,推出![]() ,可得
,可得![]() .(2)在
.(2)在![]() 中,求出OD,由
中,求出OD,由![]() ,可得
,可得![]() ,由此即可解决问题.
,由此即可解决问题.
详解:(1)证明:因为![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
故可得![]() ,
,
即可得![]() 是
是![]() 的平分线.
的平分线.
(2)因为DE是![]() 的切线,
的切线,
所以![]() ,即在
,即在![]() 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
即可得EC=4.8
点睛:本题主要考查了切线的性质及相似三角形的应用,题目难度适中,会综合运用所考查的知识点是解题的关键.
【题型】解答题
【结束】
23
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
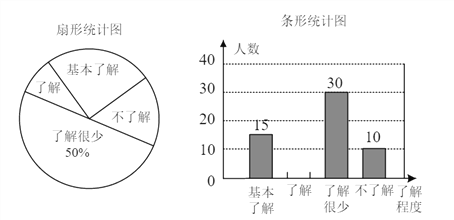
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 .
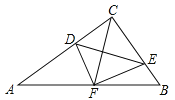
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人去南方批发茶叶,在某地A批发市场以每包m元的价格进了40包茶叶,又到B批发市场时发现同样的茶叶比A批发市场要便宜,每包的价格仅为n元,因此他又在B批发市场进了60包同样的茶叶.如果他销售时以每包![]() 元的价格全部卖出这批茶叶,那么在不考虑其它因素的情况下他的这次买卖( )
元的价格全部卖出这批茶叶,那么在不考虑其它因素的情况下他的这次买卖( )
A.一定盈利B.一定亏损
C.不盈不亏D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法感悟:
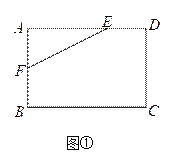
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
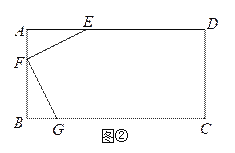
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数是﹣1,B点对应的数是1,一只小虫甲从点B出发沿着数轴的正方向以每秒4个单位的速度爬行至C点,再立即返回到A点,共用了4秒钟.
(1)求点C对应的数;
(2)若小虫甲返回到A点后再作如下运动:第1次向右爬行2个单位,第2次向左爬行4个单位,第3次向右爬行6个单位,第4次向左爬行8个单位,…依次规律爬下去,求它第10次爬行所停在点所对应的数;
(3)若小虫甲返回到A后继续沿着数轴的负方向以每秒4个单位的速度爬行,这时另一小虫乙从点C出发沿着数轴的负方向以每秒7个单位的速度爬行,设甲小虫对应的点为E点,乙小虫对应的点为F点,设点A、E、F、B所对应的数分别是xA、xE、xF、xB,当运动时间t不超过1秒时,请你结合数轴求出 |xA﹣xE |﹣|xE﹣xF |+ |xF﹣xB |= .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com