Question

【题目】如图，在ABCD中，AE⊥BC，垂足为点E，CE＝CD，点F为CE的中点，点G为CD上的一点，连接DF，EG，AG，∠1＝∠2.

(1)若CF＝2，AE＝3，求BE的长；

(2)求证：∠CEG＝∠AGE.

Answer 1

【答案】（1）（2）证明见解析

【解析】试题分析：（1）求出DC=CE=2CF=4，求出AB，根据勾股定理求出BE即可；
（2）延长AG，BC交于点H，证△CEG≌△CDF，推出CG=CF，求出M为AE中点，得出等腰三角形AGE，根据性质得出GM是∠AGE的角平分线，即可得出答案．

试题解析：(1)∵点F为CE的中点，∴CE＝CD＝2CF＝4.

又∵四边形ABCD为平行四边形，∴AB＝CD＝4.

在Rt△ABE中，由勾股定理，得BE＝＝.

(2)证明：延长AG，BC交于点H.

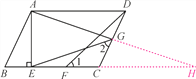
∵∠2＝∠1，∠ECG＝∠DCF，CE＝CD

∴△CEG≌△CDF(AAS)．∴CG＝CF.

∵CD＝CE＝2CF，∴CG＝GD.

∵在ABCD中，AD∥BC，

∴∠DAG＝∠CHG，∠ADG＝∠HCG.

∴△ADG≌△HCG(AAS)．∴AG＝HG.

∵∠AEH＝90°，∴EG＝AG＝HG.∴∠CEG＝∠H.

∵∠AGE＝∠CEG＋∠H，

∴∠AGE＝2∠CEG，即∠CEG＝∠AGE.