
����Ŀ��ij���ڳ��д�����У���Ҫ��ֲA��B���ֲ�ͬ�����繲3000�ã����б꣬�а�����15��Ԫ�ı����б�а�������̣����ݵ��鼰������ϱ�����A��B��������ijɱ��ۼ��ɻ��������
Ʒ�� | ����ۣ�Ԫ/�ã� | �ɻ��� |
A | 28 | 90% |
B | 40 | 95% |
����ֲA������x�ã��а��̻�õ�����ΪyԪ��
��1����y��x֮��ĺ�����ϵʽ��
��2������Ҫ����ֲ��������ijɻ��ʲ�����93%���а���Ӧ���ѡ��������ܻ�����������������Ƕ��٣�
��3���ڴﵽ��2����������Ҫ�����������ǰ���£��а������̻��ӵ�40����ֲ���������磬��֪ÿ��ÿ�����ֲA������6�û�B������3�ã���η�����������ʹ��ֲA��B��������ͬʱ�깤��
���𰸡�(1)y=150000��28x��40��3000��x��=12x+30000��0��x��3000����
(2)����A������1200�ã�B������1800��ʱ���а���Ӧ����������������Ϊ44400Ԫ��
(3)����10����ֲA�����磬30����ֲB�����磬ǡ��ͬʱ�깤��
��������
�����������1���ɹ���A������x�ã��ɵó�����B�����磨3000��x���ã����ݡ�������=���۩�����A������Ǯ��������B������Ǯ�������ɵó�y����x�ĺ�����ϵʽ��
��2����������Ҫ����ֲ��������ijɻ��ʲ�����93%�������г�����x��һԪһ�β���ʽ���ⲻ��ʽ���ɵó�x��ȡֵ��Χ���ٸ���һ�κ��������ʣ����ɽ����ֵ���⣻
��3���谲��m����ֲA�����磬���У�40��m������ֲB�����磬����ÿ��ÿ�����ֲA������6�û�B������3����ͬʱ�깤�����г�����m�ķ�ʽ���̣����ʽ�������m��ֵ������ɵó����ۣ�
�����������1���������⣬�ã�����B�����磨3000��x���ã�
��y��x֮��ĺ�����ϵʽΪy=150000��28x��40��3000��x��=12x+30000��0��x��3000����
��2���������⣬�ã�90%x+95%��3000��x����93%��3000��
��ã�x��1200��
��y=12x+30000��k=12��0��
����x=1200��3000��1200=1800ʱ��yȡ���ֵ�����ֵΪ44400��
�𣺹���A������1200�ã�B������1800��ʱ���а���Ӧ����������������Ϊ44400Ԫ��
��3���谲��m����ֲA�����磬���У�40��m������ֲB�����磬
�������⣬�ã�![]() =
=![]() ��
��
��ã�m=10��
�����飬m=10�Ƿ�ʽ���̵Ľ⣬�ҷ���ʵ�ʣ���ʱ40��10=30���ˣ���
�𣺰���10����ֲA�����磬30����ֲB�����磬ǡ��ͬʱ�깤��


 Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������֮�俪ͨ�˶���������г�����֪ÿ��2h��һ���ٶ���ͬ�Ķ������г��Ӽ׳ǿ����ҳǣ���ͼ��OA�ǵ�һ�ж������г��뿪�׳ǵ�·��s��km��������ʱ��t��h���ĺ���ͼ��BC��һ�д��ҳǿ����׳ǵ���ͨ�쳵��׳ǵ�·��s��km��������ʱ��t��h���ĺ���ͼ�������ͼ�е���Ϣ������������⣺
��1����ͼ����ͨ�쳵����ʱ��ȵ�һ�ж������г�����ʱ�� 1h������������������������B��������600��ʵ�������� ��
��2����ֱ����ͼ�л����ڶ��ж������г��뿪�׳ǵ�·��s��km����ʱ��t��h���ĺ���ͼ��
��3������ͨ�쳵���ٶ�Ϊ100km/h��
����ڶ��ж������г������ʱ�������ͨ�쳵������
����ֱ��д��������ͨ�쳵����ʻ;����ӭ��������������ж������г�������ʱ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӱ��ϵ�ʱ��ָʾΪ���㣬��ʱʱ��ͷ���֮�����γɵ�(С��ƽ��)�ǵĶ�����.
A. 120�� B. 30�� C. 60�� D. 90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л��������ǣ� ��.
A.-��-3��= 3
B.+��-3��=-3
C.-[+(-3)]= -3
D.-[-��-3��]=-3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��������ı����Ϸֱ�д��������6����������ÿ����������ϵ��������ĺͶ���ȣ�����6�������ĺ�Ϊ �� 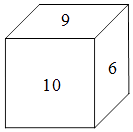
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=12cm��BC=24cm��������þ����ضԽ���BD�۵�����ôͼ����Ӱ���ֵ������ ��cm2��
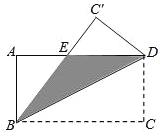
A��72 B��90 C��108 D��144
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������������ԼΪ383 900ǧ�ף���ô��������ÿ�ѧ��������ʾΪ �� ��
A. 3.839��104 ǧ�� B. 3.839��105ǧ��
C. 3.839��106ǧ�� D. 38.39��104ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD����AE��BC������Ϊ��E��CE��CD����FΪCE���е�����GΪCD�ϵ�һ��������DF��EG��AG����1����2.

(1)��CF��2��AE��3����BE�ij���
(2)��֤����CEG��![]() ��AGE.
��AGE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�� 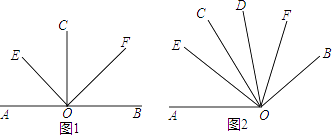
��1����ͼ1����CO��AB������ΪO��OE��OF�ֱ�ƽ�֡�AOC���BOC�����EOF�Ķ�����
��2����ͼ2������AOC=��BOD=80�㣬OE��OF�ֱ�ƽ�֡�AOD���BOC�����EOF�Ķ�����
��3������AOC=��BOD=��������BOD�Ƶ�O��ת��ʹ������OC������OD�ļн�Ϊ�£�OE��OF�ֱ�ƽ�֡�AOD���BOC������+�¡�180�㣬�����£����EOC= �� ���ú�����µĴ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com