
����Ŀ����������
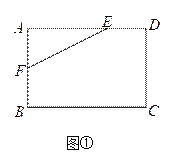
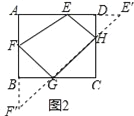
��1����ͼ�٣��ھ���ABCD�У�AB=4��AD=6��AE=4��AF=2���Ƿ��ڱ�BC��CD�Ϸֱ���ڵ�G��H��ʹ���ı���EFGH���ܳ���С�������ڣ�������ܳ�����Сֵ���������ڣ���˵�����ɣ�
��������
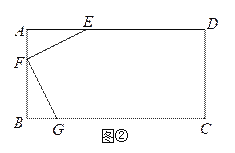
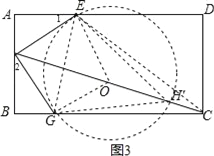
��2����ͼ�ڣ���һ���ΰ��ABCD��AB=3�ף�AD=6�ף�����Ӵ˰���вó�һ����������ܴ���ı���EFGH������ʹ��EFG=90����EF=FG=![]() �ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
�ף���EHG=45�������о���ֻ�е���E��F��G�ֱ��ڱ�AD��AB��BC�ϣ���AF��BF���������H�ھ���ABCD�ڲ������ʱ�����п��ܲó�����Ҫ��IJ����������ܷ�õ÷���Ҫ�����������ܴ���ı���EFGH���������ܣ�����õõ��ı���EFGH�������������д������BΪ����ԭ�㣬ֱ��BCΪx�ᣬֱ��BAΪy�������ϵ�У���H�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1�����ڵ��ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2�������õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() )
)
������������: ��1����E����CD�ĶԳƵ�E�䣬��F����BC�ĶԳƵ�F�䣬����E��F�䣬�õ���ʱ�ı���EFGH���ܳ���С��������ԳƵ����ʵõ�BF�䣽BF��AF��2��DE�䣽DE��2����A��90�㣬���ǵõ�AF�䣽6��AE�䣽8�����E��F�䣽10��EF��2![]() ���ɵõ����ۣ�
���ɵõ����ۣ�
��2��������ǵ����ʵõ�1����2���Ƴ���AEF�ա�BGF������ȫ�������ε����ʵõ�AF��BG��AE��BF����AF��x����AE��BF��3x���ݹ��ɶ����з��̵õ�AF��BG��1��BF��AE��2������EFG����EG�ĶԳơ�EOG�����ı���EFGO�������Σ���EOG��90�㣬��OΪԲ�ģ���EGΪ�뾶����O�����EHG��45��ĵ�H�ڡ�O�ϣ�����FO�����ӳ�����O��H�䣬��H����EG�Ĵ�ֱƽ�����ϣ�����EH��GH�䣬���EH��G��45�㣬���ǵõ��ı���EFGH���Ƿ�����������������ݾ��ε������ʽ���ɵõ����ۣ�
���:
�⣺��1�����ڣ����ɣ���E����CD�ĶԳƵ�E����
��F����BC�ĶԳƵ�F����
����E��F������BC��G����CD��H������FG��EH��
��F��G=FG��E��H=EH�����ʱ�ı���EFGH���ܳ���С��
������ã�BF��=BF=AF=2��DE��=DE=2����A=90����
��AF��=6��AE��=8��
��E��F��=10��EF=2![]() ��
��
���ı���EFGH���ܳ�����Сֵ=EF+FG+GH+HE=EF+E��F��=2![]() +10��
+10��
���ڱ�BC��CD�Ϸֱ���ڵ�G��H��
ʹ���ı���EFGH���ܳ���С����СֵΪ2![]() +10��
+10��
��2���ܲõã�
���ɣ���EF=FG=![]() ����A=��B=90������1+��AFE=��2+AFE=90����
����A=��B=90������1+��AFE=��2+AFE=90����
���1=��2��
����AEF����BGF�� 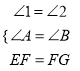 ��
��
���AEF�ա�BGF��
��AF=BG��AE=BF��
��AF=x����AE=BF=3��x��
��x2+��3��x��2=��![]() ��2��
��2��
��ã�x=1��x=2���������⣬��ȥ����
��AF=BG=1��BF=AE=2��
��DE=4��CG=5��
����EG������EFG����EG�ĶԳ���EOG��
���ı���EFGO�������Σ���EOG=90����
��OΪԲ�ģ���EGΪ�뾶����O��
���EHG=45���ĵ��ڡ�O�ϣ�
����FO�����ӳ�����O��H������H����EG�Ĵ�ֱƽ�����ϣ�
����EH��GH�������EH��G=45����
��ʱ���ı���EFGH����Ҫ��õ÷���Ҫ���������ģ�
��C���߶�EG�Ĵ�ֱƽ�����裬
���F��O��H����C��һ��ֱ���ϣ�
��EG=![]() ��
��
��OF=EG=![]() ��
��
��CF=2![]() ��
��
��OC=![]() ��
��
��OH��=OE=FG=![]() ��
��
��OH����OC��
���H���ھ���ABCD���ڲ���
������ھ���ABCD�У��õ÷�����������������ı���EFGH��������
������������=![]() EGFH��=
EGFH��=![]() ��
��![]() ����
����![]() +
+![]() ��=5+
��=5+![]() ��
��
�൱���õõ��ı��β���Ϊ�ı���EFGH��ʱ���õ��˷��������������������������Ϊ��5+![]() ��m2��H(
��m2��H(![]() +3,1��
+3,1��![]() ).
).
�㾦: ���⿼����ȫ�������ε��ж������ʣ����ε����ʣ����ɶ�������ԳƵ����ʣ����������⣬���յ��������������öԳƵ����ʽ�������ǽ���Ĺؼ���


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧԭ�ƻ��ӹ�һ��У�������мס������������ӹ�����У������֪����ÿ���ܼӹ�����У��16�����ҹ���ÿ��ӹ�����У��24�����ҵ����ӹ�����У���׳����ҳ�Ҫ����20��
��1��������У�����ж��ټ���
��2��Ϊ�˾����������У���������ɼס�����������ԭ�ٶȺ���һ��ʱ�����ͣ�������ҹ���ÿ����ٶ����25%���ҹ����������ʣ�µIJ��֣����ҹ���ȫ������ʱ���Ǽ�������ʱ���2������4�죬���ҹ����ӹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
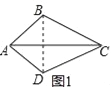
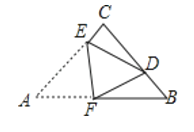
����Ŀ����ͼ������ABC�У� ![]() , AC=BC=3, ����ABC�۵���ʹ��A����BC ���ϵĵ�D����EFΪ�ۺۣ���AE=2����
, AC=BC=3, ����ABC�۵���ʹ��A����BC ���ϵĵ�D����EFΪ�ۺۣ���AE=2����![]() ��ֵΪ_____________.
��ֵΪ_____________.
���𰸡�![]()
������������������D��DG![]() AB�ڵ�G.�����۵����ʣ��ɵ�AE=DE=2��AF=DF��CE=1��
AB�ڵ�G.�����۵����ʣ��ɵ�AE=DE=2��AF=DF��CE=1��
��Rt��DCE�У��ɹ��ɶ������![]() ������DB=
������DB=![]() ����Rt��ABC�У��ɹ��ɶ�����
����Rt��ABC�У��ɹ��ɶ�����![]() ����Rt��DGB�У���������Ǻ������
����Rt��DGB�У���������Ǻ������![]() ��
�� ![]() ��
��
��AF=DF=x����FG= ![]() ����Rt��DFG�У����ݹ��ɶ����÷���
����Rt��DFG�У����ݹ��ɶ����÷���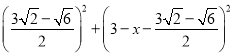 =
=![]() �����
�����![]() ���Ӷ����
���Ӷ����![]() .��ֵ
.��ֵ
��⣺
��ͼ��ʾ������D��DG![]() AB�ڵ�G.
AB�ڵ�G.

�����۵����ʣ���֪��AEF![]() ��DEF��
��DEF��
��AE=DE=2��AF=DF��CE=AC-AE=1��
��Rt��DCE�У��ɹ��ɶ�����![]() ��
��
��DB=![]() ��
��
��Rt��ABC�У��ɹ��ɶ�����![]() ��
��
��Rt��DGB�� ![]() ��
�� ![]() ��
��
��AF=DF=x����FG=AB-AF-GB=![]() ��
��
��Rt��DFG���� ![]() ��
��
��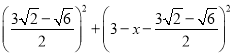 =
=![]() ��
��
���![]() ��
��
��![]() =
=![]() =
=![]() .
.
�ʴ�Ϊ�� ![]() .
.
�㾦����Ҫ�����˷��۱任�����ʡ����ɶ�����������������Ķ��壻����Ĺؼ�����������۵������ʡ����ɶ�����������Ǻ����Ķ����֪ʶ��������⣮
�����͡������
��������
18
����Ŀ���涨��[x]��ʾ������x ����������(x) ��ʾ��С��x����С������[x) ��ʾ��ӽ�x��������x��n+0.5��nΪ�����������磺[2.3]=2��(2.3)=3��[2.3)=2��������˵����ȷ����__________��д��������ȷ˵����.
�ٵ�x=1.7ʱ��[x]+(x)+[x)=6��
�ڵ�x=-2.1ʱ��[x]+(x)+[x)=-7��
�۷���4[x]+3(x)+[x)=11�Ľ�Ϊ1<x<1.5��
�ܵ�-1<x<1ʱ, ����y=[x]+(x)+x ��ͼ��y=4x ��ͼ������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��ֽ�ƣ��քe�Ǻ���3������4�ͺ���5����ƺ�3����4����5��������ϴ�Ⱥ���ȳ�ȡһ�ţ����»�ɫ�����ֺ��ƷŻأ�ϴ�Ⱥ����ٳ�ȡһ�ţ�
��1�����γ��ֽ�ƾ�Ϊ���ҵĸ��ʣ�������������״ͼ�������б����ȷ���д���������̣�
��2���ס�����������Ϸ���������ַ�����A�����������γ����ɫ��ͬ���ʤ��������ʤ��B�����������γ��ֽ�Ƶ����ֺ�Ϊ�������ʤ��������ʤ�����ʼ�ѡ�����ַ���ʤ�ʸ��ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���A=90����
��1������Բ���ֱ��������P��ʹԲ��P��AC���ϣ�����AB��BC���߶����У�������ͼ�ۼ�����д������֤������

��2���ڣ�1���������£�����B=45����AB=1����P��BC�ڵ�D�����ӻ�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪѡ��һ��ѡ�ֲμ����������ţ���Ϊ�����������������ݽ����������о�������ͼ��ʾ����Ŀ��Ȩ����ѡ��������ѡ�ֽ��п��������Ű�ԭ��ͳ��ͼ�����������±����������Ż���ѡ�����еĵ÷������

��װ | ��ͨ�� | ���� | �ݽ����� | |
���� | 85 | 70 | 80 | 85 |
�Ż� | 90 | 75 | 75 | 80 |
���������Ϣ���ش��������⣺
��1�����װ��Ŀ��ѡ�ֿ����е�Ȩ����
��2����������ѧ��֪ʶ������ѧУ���������Ż�������ѡ��һ�˲μ����������ţ���Ϊ�����������������ݽ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���֪EΪBC���е㣬����AE���ӳ���DC���ӳ����ڵ�F������BF��
��1����֤��AB=CF��
��2����BC��AF����ʲô������ϵʱ���ı���ABFC�Ǿ��Σ���˵�����ɣ�
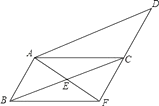
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A(a ,2![]() )��ֱ��y=
)��ֱ��y=![]() x��һ�㣬��AΪԲ�ģ�2Ϊ�뾶����A����P(x,y)�ǵ�һ�����ڡ�A������һ�㣬��
x��һ�㣬��AΪԲ�ģ�2Ϊ�뾶����A����P(x,y)�ǵ�һ�����ڡ�A������һ�㣬��![]() ����СֵΪ�� ��
����СֵΪ�� ��
A. 1 B. ![]() C.
C. ![]() ��1 D.
��1 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ɸ���ȫ��ͬ��С��������ɵ�һ�������塣
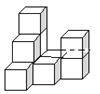
��1��ͼ������ ����С�����壻
��2���뻭����������������ͼ����ͼ��������Ӱ��ʾ��
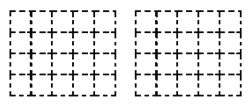
��3������������������������һЩ��ͬ��С�����壬���������������ĸ���ͼ������ͼ���䣬��ô�����������Ӽ���С�����壿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com