练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（　　）

    ①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上．

    A. B. C. D.

    【答案】C

    【解析】

    直接利用直线的性质以及线段的性质分析得出答案．

    ①用两颗钉子就可以把木条固定在墙上，可以用基本事实“两点确定一条直线”来解释；

    ②把笔尖看成一个点，当这个点运动时便得到一条线，可以用基本事实“无数个点组成线”来解释；

    ③把弯曲的公路改直，就能缩短路程，可以用基本事实“两点之间线段最短”来解释；

    ④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上，可以用基本事实“两点确定一条直线”来解释．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图：在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式x2y4的次数为c.

    (1)a=___，b=___，c=___；

    (2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”)；

    (3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示)；

    (4)请问：3ABBC的值是否随着时间t的变化而改变?若变化，请说明理由；若不变，请求其值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，，角平分线交BC于O，以OB为半径作⊙O.（1）判定直线AC是否是⊙O的切线，并说明理由;

    （2）连接AO交⊙O于点E，其延长线交⊙O于点D，，求的值;

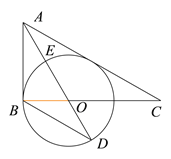
    （3）在（2）的条件下，设的半径为3，求AC的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上两点、，其中A表示的数为-2，表示的数为2，若在数轴上存在一点，使得，则称点叫做点、的“节点”，例如图1所示，若点表示的数为0，有，则称点为点、的“4节点”.

    请根据上述规定回答下列问题：

    （1）若点为点、的“节点”，且点在数轴上表示的数为-4，求的值.

    （2）若点是数轴上点、的“5节点”，请你直接写出点表示的数为____________；

    （3）若点在数轴上（不与、重合），满足、之间的距离是、之间距离的一半，且此时点为点、的“节点”，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐示系xOy中，直线与直线交于点A(3，m).

    (1)求k，m的値；

    (2)己知点P(n，n)，过点P作垂直于y轴的直线与直线交于点M，过点P作垂直于x轴的直线与直线交于点N(P与N不重合).若PN≤2PM，结合图象，求n的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

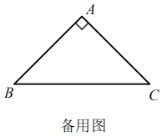
    【题目】在RtΔABC中，∠BAC=90°，点O是△ABC所在平面内一点，连接OA，延长OA到点E，使得AE=OA，连接OC，过点B作BD与OC平行，并使∠DBC=∠OCB，且BD=OC，连接DE.

    (1)如图一，当点O在RtΔABC内部时.

    ①按题意补全图形；

    ②猜想DE与BC的数量关系，并证明.

    (2)若AB=AC(如图二)，且∠OCB=30°，∠OBC=15°，求∠AED的大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

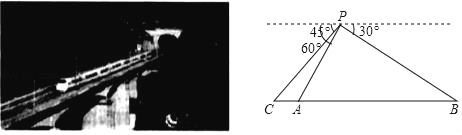
    【题目】宜万铁路线上，一列列和谐号动车象一条条巨龙穿梭于恩施崇山峻岭，大多地段桥梁与隧道交替相连如图，勘测队员在山顶P处测得山脚下隧道入口A点处的俯角为60°，隧道出口B点处的俯角为30°，一列动车以180km/h的速度自西向东行驶，当车头抵达入口A点处时，车尾C点处的俯角是45°，整个车身全部进入隧洞恰好用了4s钟时间，求车身完全在隧道中运行的时间（结果精确到1秒，参考数据：≈1.414，≈1.732 ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D．

    （1）求证：AC平分∠DAB；

    （2）过点O作线段AC的垂线OE，垂足为E（要求：尺规作图，保留作图痕迹，不写作法）；

    （3）若CD=4，AC=4，求垂线段OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，二次函数y=mx2－(2m+1)x+m－5的图象与x轴有两个公共点．

    （）求m的取值范围；

    （）若m取满足条件的最小的整数，

    ①写出这个二次函数的表达式；

    ②当n≤x≤1时，函数值y的取值范围是－6≤y≤4－n，求n的值；

    ③将此二次函数图象平移，使平移后的图象经过原点O．设平移后的图象对应的函数表达式为y=a(x－h)2 +k，当x<2时，y随x的增大而减小，求k的取值范围．

    查看答案和解析>>

    同步练习册答案