
【题目】在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(![]() )求m的取值范围;
)求m的取值范围;
(![]() )若m取满足条件的最小的整数,
)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]() ;
;![]() ③
③![]()
【解析】分析:(1)因为函数为二次函数,所以有m≠0,又因为图象与![]() 轴有两个交点,所以判别式△>0,联立即可解得
轴有两个交点,所以判别式△>0,联立即可解得![]() 的范围。
的范围。
(2)①因为m>-![]() 且m≠0,且m取满足条件的最小的整数,所以m=1,所以二次函数的解析式为
且m≠0,且m取满足条件的最小的整数,所以m=1,所以二次函数的解析式为![]() ;
;
②因为二次函数的对称轴为直线x=![]() ,所以n≤x≤1时,y随x的增大而减小,当x=1时,函数值为-6,当x=n时,函数值为4-n,即可得到关于n的一元二次方程,求解即可;
,所以n≤x≤1时,y随x的增大而减小,当x=1时,函数值为-6,当x=n时,函数值为4-n,即可得到关于n的一元二次方程,求解即可;
③由平移后图象对应的函数表达式可得a=1,因为平移后的图象经过原点O,将点(0,0)代入平移后的函数表达式可得k=-![]() ,由x<2,y
,由x<2,y![]() 随x的增大而减小得对称轴h≥2,即可确定k的取值范围。
随x的增大而减小得对称轴h≥2,即可确定k的取值范围。
详解:(1)![]()
∵该二次函数图像与x轴有两个交点
∴![]()
(2)①![]()
②![]()
函数对称轴是直线x=1.5
因为在n≤x≤1范围内,x=n时y取到最大值![]()
而当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n
所以![]()
得n=-2或n=4(不合题意)
③由题意得a=1,图象经过原点,可得![]()
∵当x<2时,y随x的增大而减小
∴![]()
则![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0) ,与过A点的直线相交于另一点D(3,![]() ) ,过点D作DC⊥x轴,垂足为C.
) ,过点D作DC⊥x轴,垂足为C.
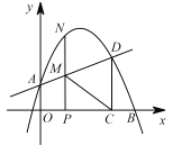
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM 面积的最大值;
(3)若P 是x 轴正半轴上的一动点,设OP 的长为t.是否存在t,使以点M,C,D,N 为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,直线a经过点A,且BE⊥a于E,DF⊥a于F.
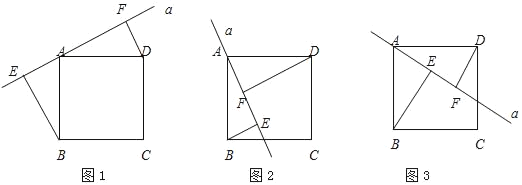
(1)当直线a绕点A旋转到图1的位置时,求证:①△ABE≌△DAF;②EF=BE+DF;
(2)当直线a绕点A旋转到图2的位置时,试探究EF、BE、DF具有怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线a绕点A旋转到图3的位置时,试问DF、EF、BE具有怎样的等量关系?请写出这个等量关系,不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 交于点A,点A的横坐标为
交于点A,点A的横坐标为![]() ,且直线
,且直线![]() 与x轴交于点B,与y轴交于点D,直线
与x轴交于点B,与y轴交于点D,直线![]() 与y轴交于点C.
与y轴交于点C.
(1)求点A的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
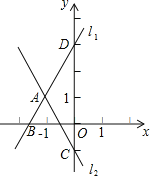
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为A(![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
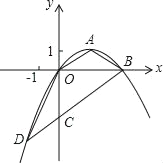
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
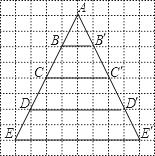
【题目】如图,△ACC′是由△ABB′经过位似变换得到的
(1)求出△ACC′与△ABB′的相似比,并指出它们的位似中心;
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为3,那么△ABB′的位似图形是什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com