Question

【题目】如图，正方形ABCD中，直线a经过点A，且BE⊥a于E，DF⊥a于F．

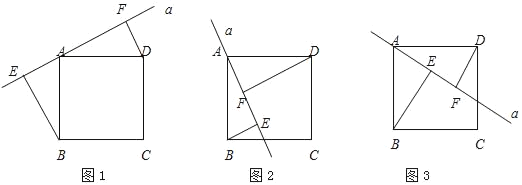
（1）当直线a绕点A旋转到图1的位置时，求证：①△ABE≌△DAF；②EF＝BE+DF；

（2）当直线a绕点A旋转到图2的位置时，试探究EF、BE、DF具有怎样的等量关系？请写出这个等量关系，并加以证明；

（3）当直线a绕点A旋转到图3的位置时，试问DF、EF、BE具有怎样的等量关系？请写出这个等量关系，不证明．

Answer 1

【答案】（1）①见解析；②见解析；（2）EF＝DF﹣BE，理由见解析；（3）EF＝BE﹣DF，理由见解析

【解析】

（1）①由正方形的性质得出AB＝AD，∠BAD＝90°，证出∠ABE＝∠DAF，由ASA证明△ABE≌△DAF即可；

②由全等三角形的性质得出BE＝AF，AE＝DF，即可得出结论；

（2）由正方形的性质得出AB＝AD，∠BAD＝90°，证出∠ABE＝∠DAF，由ASA证明△ABE≌△DAF，得出BE＝AF，AE＝DF，即可得出结论；

（3）由正方形的性质得出AB＝AD，∠BAD＝90°，证出∠ABE＝∠DAF，由ASA证明△ABE≌△DAF，得出BE＝AF，AE＝DF，即可得出结论．

（1）证明：①∵四边形ABCD是正方形，

∴AB＝AD，∠BAD＝90°．

∴∠BAE+∠DAF＝90°，

又∵BE⊥a，DF⊥a，

∴∠AEB＝∠DFA＝90°，

∴∠BAE+∠ABE＝90°，

∴∠ABE＝∠DAF，

在△ABE和△DAF中，

，

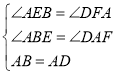∴△ABE≌△DAF（AAS）．

②∵△ABE≌△DAF，

∴BE＝AF，AE＝DF，

∵EF＝AF+AE，

∴EF＝BE+DF；

（2）解：EF＝DF﹣BE，理由如下：

∵四边形ABCD是正方形

∴AB＝AD，∠BAD＝90°，∴∠BAE+∠DAF＝90°，

又∵BE⊥a，DF⊥a，

∴∠AEB＝∠DFA＝90°，

∴∠BAE+∠ABE＝90°，

∴∠ABE＝∠DAF，在△ABE和△DAF中，

，

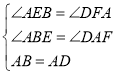∴△ABE≌△DAF（AAS）．

∴AE＝DF，BE＝AF，

又∵EF＝AE﹣AF，

∴EF＝DF﹣BE；

（3）解：EF＝BE﹣DF；理由如下：

同（2）得：△ABE≌△DAF（AAS）．

∴AE＝DF，BE＝AF，

又∵EF＝AF﹣AE，

∴EF＝BE﹣DF．