
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为________.
,那么该矩形的周长为________.

【答案】72cm
【解析】在矩形ABCD中,AB=CD,AD=BC,∠B=∠D=90°,
∵△ADE沿AE对折,点D的对称点F恰好落在BC上,
∴∠AFE=∠D=90°,AD=AF,
∵∠EFC+∠AFB=180°-90°=90°,
∠BAF+∠AFB=90°,
∴∠BAF=∠EFC,
∵tan∠EFC=![]() ,
,
∴设BF=3x、AB=4x,
在Rt△ABF中,AF=![]() =5x,
=5x,
∴AD=BC=5x,
∴CF=BC-BF=5x-3x=2x,
∵tan∠EFC=![]() ,
,
∴CE=CFtan∠EFC=2x![]() =
=![]() x,
x,
∴DE=CD-CE=4x-![]() x=
x=![]() x,
x,
在Rt△ADE中,AD2+DE2=AE2,
即(5x)2+(![]() x)2=(10
x)2=(10![]() )2,
)2,
整理得,x2=16,
解得x=4,
∴AB=4×4=16cm,AD=5×4=20cm,
矩形的周长=2×(16+20)=72cm,
故答案为:72cm.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,直线a经过点A,且BE⊥a于E,DF⊥a于F.
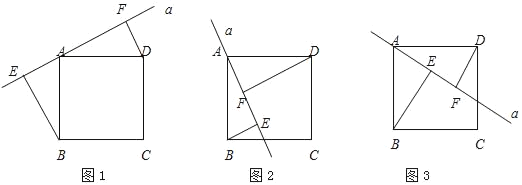
(1)当直线a绕点A旋转到图1的位置时,求证:①△ABE≌△DAF;②EF=BE+DF;
(2)当直线a绕点A旋转到图2的位置时,试探究EF、BE、DF具有怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线a绕点A旋转到图3的位置时,试问DF、EF、BE具有怎样的等量关系?请写出这个等量关系,不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4![]() ,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.
,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
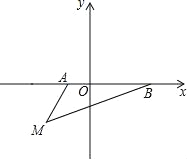
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“清明小假期”举行促销活动,设立了一个可以自由转动的转盘进行摇奖活动,并规定顾客每购买200元商品,就可以获得一次转动转盘的机会,小明根据活动情况绘制了一个扇形统计图,如图所示.
(1)求每转动一次转盘所获得购物券金额的平均数;
(2)小明做了一次实验,他转了200次转盘,总共获得5800元购物券,他平均每转动一次转盘获得的购物券是多少元?
(3)请你说明上述两个结果为什么有差别?

查看答案和解析>>
科目:初中数学 来源: 题型:
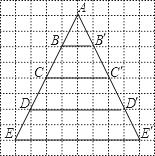
【题目】如图,△ACC′是由△ABB′经过位似变换得到的
(1)求出△ACC′与△ABB′的相似比,并指出它们的位似中心;
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为3,那么△ABB′的位似图形是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们学过有理数减法可以转化为有理数加法来运算,有理数除法可以转化为有理数乘法来运算.其实这种转化的数学方法,在学习数学时会经常用到,通过转化我们可以把一个复杂问题转化为一个简单问题来解决.
例如:计算![]()
此题我们按照常规的运算方法计算比较复杂,但如果采用下面的方法把乘法转化为减法后计算就变得非常简单.
分析方法:
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,将以上4个等式两边分别相加即可得到结果,解法如下:
![]()
=![]()
=![]()
=![]()
(1)![]() =
=
(2)应用上面的方法计算:![]() ;
;
(3)类比应用上面的方法探究并计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
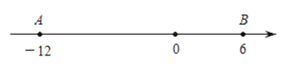
【题目】如图,数轴上![]() 两点开始时所对应的数分别是
两点开始时所对应的数分别是![]() 和6.
和6.![]() 两点各自以一定的速度在数轴上运动,且
两点各自以一定的速度在数轴上运动,且![]() 点的运动速度为2个单位长度∕秒.
点的运动速度为2个单位长度∕秒.
(1)若点![]() 为
为![]() 两点初始时线段
两点初始时线段![]() 的中点,则点
的中点,则点![]() 所表示的数是_____;
所表示的数是_____;
(2)![]() 两点同时出发相向而行,在原点处相遇,求
两点同时出发相向而行,在原点处相遇,求![]() 点的运动速度;
点的运动速度;
(3)若![]() 两点按(2)中的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?
两点按(2)中的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com