
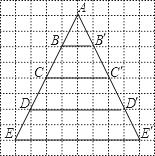
【题目】如图,△ACC′是由△ABB′经过位似变换得到的
(1)求出△ACC′与△ABB′的相似比,并指出它们的位似中心;
(2)△AEE′是△ABB′的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为3,那么△ABB′的位似图形是什么?
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(![]() )求m的取值范围;
)求m的取值范围;
(![]() )若m取满足条件的最小的整数,
)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为________.
,那么该矩形的周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,CA=CB,∠ACB=90°,点O是AB的中点.
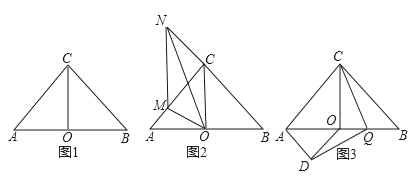
(1)如图1,求证:CO=BO;
(2)如图2,点M在边AC上,点N在边BC延长线上,MN﹣AM=CN,求∠MON的度数;
(3)如图3,AD∥BC,OD∥AC,AD与OD交于点D,Q是OB的中点,连接CQ、DQ,试判断线段CQ与DQ的关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为20cm2,对角线交于点O,以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B…依此类推,则平行四边形AO2019C2020B的面积为( )cm2.

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
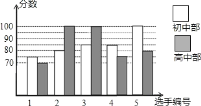
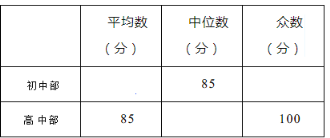
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家买了一辆小轿车,小明连续记录了一周每天行驶的路程:

请你用学过的统计知识解决下面的问题:
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.64元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元(精确到百位).
查看答案和解析>>
科目:初中数学 来源: 题型:
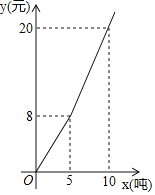
【题目】随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示生活用水费(元).请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按 元收取;超过5吨的部分,每吨按 元收取;
(2)请写出居民使用5吨水以内y与x的关系式;
(3)若小明家这个月交水费32元,他家本月用了多少吨水?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com