
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4![]() ,求垂线段OE的长.
,求垂线段OE的长.

【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)连接OC,由CD为圆O的切线,根据切线性质得到OC与CD垂直,又AD与CD垂直,根据平面上垂直于同一条直线的两直线平行得到AD与OC平行,由平行得一对内错角相等,又因为两半径OA与OC相等,根据等边对等角,得到一对相等的角,利用等量代换,即可得到∠DAC=∠OAC,即AC为∠DAB的平分线;
(2)以O为圆心,以大于O到AC的距离为半径画弧,与AC交于两点,分别以这两点为圆心,以大于这两点之间距离的一半长为半径在AC的另一侧画弧,两弧交于一点,经过此点与点O确定一条直线,即为所求的直线,如图所示;
(3)在直角三角形ACD中,由CD和AC的长,利用勾股定理求出AD的长,再根据垂径定理,由OE与AC 垂直,得到E为AC中点,求出AE的长,由(1)推出的角平分线得一对角相等,再由一对直角相等,根据两对对应角相等的两三角形相似,由相似得比例即可求出OE的长.
试题解析:(1)证明:连接OC.∵CD切⊙O于点C,∴OC⊥CD.又∵AD⊥CD,∴OC∥AD,∴∠OCA=∠DAC.∵OC=OA,∴∠OCA=∠OAC,∴∠OAC=∠DAC,∴AC平分∠DAB;
(2)解:点O作线段AC的垂线OE如图所示:
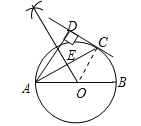
∴直线OE所求的直线;
(3)解:在Rt△ACD中,CD=4,AC=4![]() ,∴AD=
,∴AD=![]() =
=![]() =8.∵OE⊥AC,∴AE=
=8.∵OE⊥AC,∴AE=![]() AC=2
AC=2![]() .∵∠OAE=∠CAD,∠AEO=∠ADC,∴△AEO∽△ADC,∴
.∵∠OAE=∠CAD,∠AEO=∠ADC,∴△AEO∽△ADC,∴![]() =
=![]() ,∴OE=
,∴OE=![]() ×CD=
×CD=![]() ×4=
×4=![]() .即垂线段OE的长为
.即垂线段OE的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】计算题
(1)30-(-12)-(-25)-18+(-10)
(2) (-![]() +
+![]() -
-![]() )
)![]()
![]() .
.
(3)-52÷(-3)2×(-5)3÷[-(-5)2]
(4)(-2![]() +3
+3![]() )-(2
)-(2![]() -
-![]() )+6
)+6![]()
(5)![]()
![]() -[
-[![]() (
(![]() -
-![]() )+4
)+4![]() ]-
]-![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
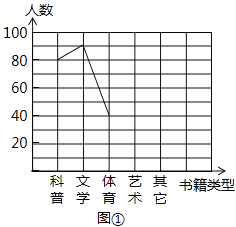
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),将线段AB先向上平移2个单位长度,再向右平移1个单位长度,得到线段CD,连接AC,BD,构成平行四边形ABDC.
(1)请写出点C的坐标为 ,点D的坐标为 ,S四边形ABDC ;
(2)点Q在y轴上,且S△QAB=S四边形ABDC,求出点Q的坐标;
(3)如图(2),点P是线段BD上任意一个点(不与B、D重合),连接PC、PO,试探索∠DCP、∠CPO、∠BOP之间的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0) ,与过A点的直线相交于另一点D(3,![]() ) ,过点D作DC⊥x轴,垂足为C.
) ,过点D作DC⊥x轴,垂足为C.
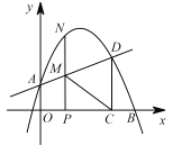
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM 面积的最大值;
(3)若P 是x 轴正半轴上的一动点,设OP 的长为t.是否存在t,使以点M,C,D,N 为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,直线a经过点A,且BE⊥a于E,DF⊥a于F.
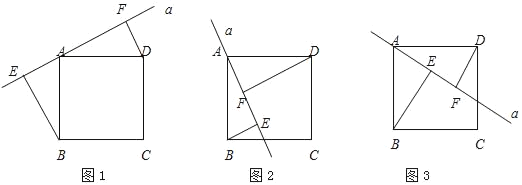
(1)当直线a绕点A旋转到图1的位置时,求证:①△ABE≌△DAF;②EF=BE+DF;
(2)当直线a绕点A旋转到图2的位置时,试探究EF、BE、DF具有怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线a绕点A旋转到图3的位置时,试问DF、EF、BE具有怎样的等量关系?请写出这个等量关系,不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com