
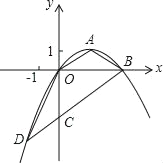
【题目】如图,顶点为A(![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x;(2)见解析;(3)点P的坐标为(﹣
x;(2)见解析;(3)点P的坐标为(﹣![]() ,0)
,0)
【解析】试题分析:(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y=![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y=![]() x﹣2.最后求出交点坐标C,D即可;
x﹣2.最后求出交点坐标C,D即可;
(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
试题解析:解:(1)∵抛物线顶点为A(![]() ,1),设抛物线解析式为y=a(x﹣
,1),设抛物线解析式为y=a(x﹣![]() )2+1,将原点坐标(0,0)在抛物线上,∴0=a(
)2+1,将原点坐标(0,0)在抛物线上,∴0=a(![]() )2+1
)2+1
∴a=﹣![]() ,∴抛物线的表达式为:y=﹣
,∴抛物线的表达式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)令y=0,得 0=﹣![]() x2+
x2+![]() x,∴x=0(舍),或x=2
x,∴x=0(舍),或x=2![]()
∴B点坐标为:(2![]() ,0),设直线OA的表达式为y=kx.∵A(
,0),设直线OA的表达式为y=kx.∵A(![]() ,1)在直线OA上,∴
,1)在直线OA上,∴![]() k=1,∴k=
k=1,∴k=![]() ,∴直线OA对应的一次函数的表达式为y=
,∴直线OA对应的一次函数的表达式为y=![]() x.
x.
∵BD∥AO,设直线BD对应的一次函数的表达式为y=![]() x+b.∵B(2
x+b.∵B(2![]() ,0)在直线BD上,∴0=
,0)在直线BD上,∴0=![]() ×2
×2![]() +b,∴b=﹣2,∴直线BD的表达式为y=
+b,∴b=﹣2,∴直线BD的表达式为y=![]() x﹣2.
x﹣2.
由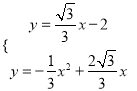
得交点D的坐标为(﹣![]() ,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2
,﹣3),令x=0得,y=﹣2,∴C点的坐标为(0,﹣2),由勾股定理,得:OA=2=OC,AB=2=CD,OB=2![]() =OD.
=OD.
在△OAB与△OCD中, 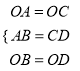 ,∴△OAB≌△OCD.
,∴△OAB≌△OCD.
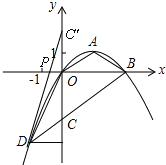
(3)点C关于x轴的对称点C'的坐标为(0,2),∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,∴PO∥DQ,∴△C'PO∽△C'DQ,∴![]() ,∴
,∴![]() ,∴PO=
,∴PO=![]() ,∴点P的坐标为(﹣
,∴点P的坐标为(﹣![]() ,0).
,0).


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
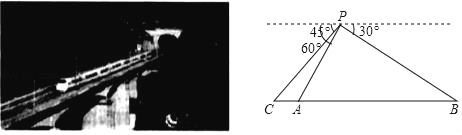
【题目】宜万铁路线上,一列列和谐号动车象一条条巨龙穿梭于恩施崇山峻岭,大多地段桥梁与隧道交替相连如图,勘测队员在山顶P处测得山脚下隧道入口A点处的俯角为60°,隧道出口B点处的俯角为30°,一列动车以180km/h的速度自西向东行驶,当车头抵达入口A点处时,车尾C点处的俯角是45°,整个车身全部进入隧洞恰好用了4s钟时间,求车身完全在隧道中运行的时间(结果精确到1秒,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732 ).
≈1.732 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(![]() )求m的取值范围;
)求m的取值范围;
(![]() )若m取满足条件的最小的整数,
)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
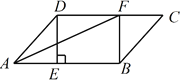
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
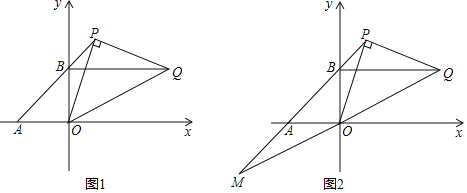
【题目】已知:如图,直线AB交两坐标轴于A(a,0)、B(0,b)两点,且a,b满足等式:![]() +(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
+(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
(1)求A,B两点的坐标;
(2)当P点在直线AB上的第一象限内运动时,![]() AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
(3)延长QO与直线AB交于点M.请判断出线段AP,BM,PM三条线段构成三角形的形状,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.

(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?
②是否存在满足条件的点P,使得PC=![]() ?(不需说明理由).
?(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
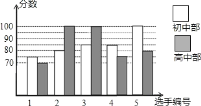
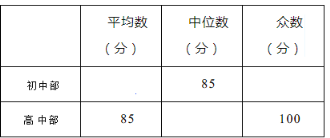
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com