
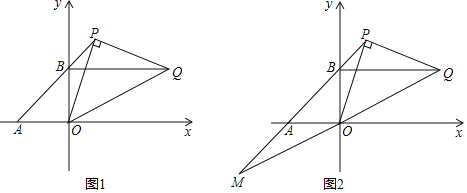
【题目】已知:如图,直线AB交两坐标轴于A(a,0)、B(0,b)两点,且a,b满足等式:![]() +(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
+(b﹣4)2=0,点P为直线AB上第一象限内的一动点,过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q,
(1)求A,B两点的坐标;
(2)当P点在直线AB上的第一象限内运动时,![]() AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
AP﹣BQ的值变不变?如果不变,请求出这个定值;若变化请说明理由.
(3)延长QO与直线AB交于点M.请判断出线段AP,BM,PM三条线段构成三角形的形状,说明理由.
【答案】(1) A(﹣4,0)、B(0,4);(2)见解析;(3)见解析.
【解析】
(1)由![]() +(b-4)2直接可求a=-4,b=4;
+(b-4)2直接可求a=-4,b=4;
(2)过点P作PN⊥AP,交x轴于点N,连接QN,则AN=![]() AP,根据角的关系可证QM⊥ON,BQ=ON,
AP,根据角的关系可证QM⊥ON,BQ=ON,![]() AP-BQ=AN-ON=AO=4;
AP-BQ=AN-ON=AO=4;
(3)直线AB的解析式y=x+4,设P(m,4+m),分别求出直线PO的解析式为y=![]() x,直线PQ的解析式y=-
x,直线PQ的解析式y=-![]() x+
x+![]() ,根据Q点纵坐标与B点纵坐标相同,可求Q(2m+4,4),求出OQ的直线解析式为y=
,根据Q点纵坐标与B点纵坐标相同,可求Q(2m+4,4),求出OQ的直线解析式为y=![]() x,M(
x,M(![]() ,
,![]() ),分别将边表示出来PA2=2(m+4)2,BM2=2
),分别将边表示出来PA2=2(m+4)2,BM2=2![]() ,PM2=2
,PM2=2 ,利用勾股定理即可求解;
,利用勾股定理即可求解;
(1)![]() +(b﹣4)2,
+(b﹣4)2,
∴a=﹣4,b=4,
∴A(﹣4,0)、B(0,4);
(2)如图1:过点P作PN⊥AP,交x轴于点N,连接QN,
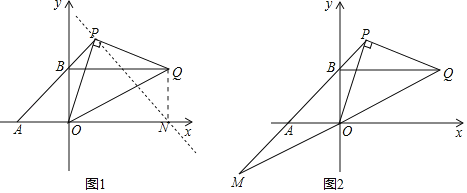
∵AO=BO=4,
∴∠PAN=45°,
∴AN=![]() AP,
AP,
∵∠BOP=∠PQO,
∴∠PQO+∠PON=90°,
∵∠OPQ=90°,
∴∠BQN+∠QNO=180°,
∵BQ∥ON,
∴QM⊥ON,
∴BQ=ON,
∴![]() AP﹣BQ=AN﹣ON=AO=4;
AP﹣BQ=AN﹣ON=AO=4;
(3)直线AB的解析式y=x+4,
设P(m,4+m),
直线PO的解析式为y=![]() x,
x,
∴直线PQ的解析式y=﹣![]() x+
x+![]() ,
,
∵Q点纵坐标为4,
∴4=﹣![]() x+
x+![]() 时,x=2m+2,
时,x=2m+2,
Q(2m+4,4),
∴OQ的直线解析式为y=![]() x,
x,
当![]() x=x+4时,x=
x=x+4时,x=![]() ,
,
∴M(![]() ,
,![]() )
)
∴PA2=2(m+4)2,
BM2=2![]() ,
,
PM2=2 ,
,
∴PA2+BM2=PM2,
∴线段AP,BM,PM三条线段构成三角形直角三角形;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
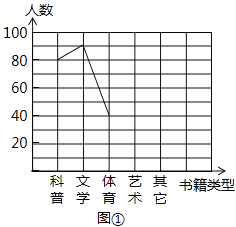
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;

(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 交于点A,点A的横坐标为
交于点A,点A的横坐标为![]() ,且直线
,且直线![]() 与x轴交于点B,与y轴交于点D,直线
与x轴交于点B,与y轴交于点D,直线![]() 与y轴交于点C.
与y轴交于点C.
(1)求点A的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
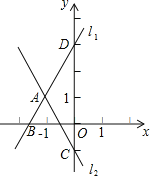
查看答案和解析>>
科目:初中数学 来源: 题型:
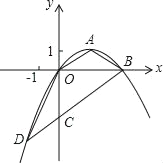
【题目】如图,顶点为A(![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
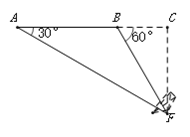
【题目】如图,在一次空中搜寻中,水平飞行的飞机观测到在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
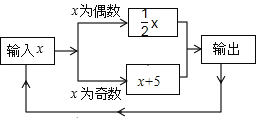
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是______,依次继续下去…,第2019输出的结果是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
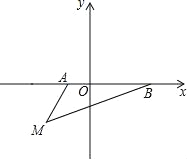
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com