[题目]解方程:(1)3x+7=32-2x(2) (3)(4)x的5倍与2的和等于x的3倍与4的差.求x, 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】解方程：

（1）3x+7=32-2x

（2）

（3）

（4）x的5倍与2的和等于x的3倍与4的差，求x；

【答案】（1）；（2）；（3）；（4）

【解析】

根据等式的性质，对方程进行去分母、去括号、合并同类项，求得x的值；对于（4），根据题意，列出方程，再求解即可.

（1）3x+7=32-2x

解：移项得：3x+2x=32-7

合并同类项得：5x=25

解得：x=5

（2）

解：去括号得：4x+6x-9=12-x-4

移项得：4x+6x+x=12-4+9

合并同类项得：11x=17

解得：

（3）

解：去分母得：4（5y+4）+3（y-1）=24-（5y-5）

去括号得：20y+16+3y-3=24-5y+5

合并同类项得：23y+13=29-5y

移项得：23y+5y=29-13

合并同类项得：28y=16

解得：

（4）x的5倍与2的和等于x的3倍与4的差，求x；

解：由题意得：5x+2=3x-4

2x=-6

x=-3

练习册系列答案

中考研究全国各省市中考真题常考基础题系列答案

每日10分钟口算心算速算天天练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

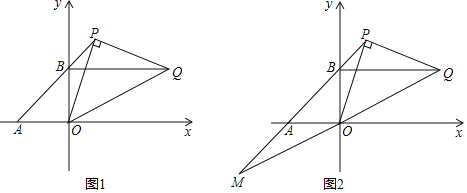
【题目】已知：如图，直线AB交两坐标轴于A（a，0）、B（0，b）两点，且a，b满足等式：+（b﹣4）2＝0，点P为直线AB上第一象限内的一动点，过P作OP的垂线且与过B点且平行于x轴的直线相交于点Q，

（1）求A，B两点的坐标；

（2）当P点在直线AB上的第一象限内运动时，AP﹣BQ的值变不变？如果不变，请求出这个定值；若变化请说明理由．

（3）延长QO与直线AB交于点M．请判断出线段AP，BM，PM三条线段构成三角形的形状，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】等腰Rt△ABC中，CA＝CB，∠ACB＝90°，点O是AB的中点．

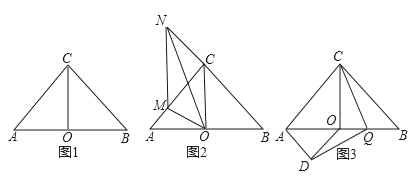
（1）如图1，求证：CO＝BO；

（2）如图2，点M在边AC上，点N在边BC延长线上，MN﹣AM＝CN，求∠MON的度数；

（3）如图3，AD∥BC，OD∥AC，AD与OD交于点D，Q是OB的中点，连接CQ、DQ，试判断线段CQ与DQ的关系，并给出证明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我市某中学举行“中国梦校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.

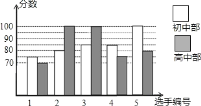
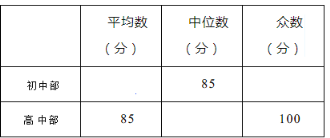
(1)根据图示填写下表；

(2)结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线的解析表达式为，且与轴交于点D,直线经过点A,B,直线，交于点C．

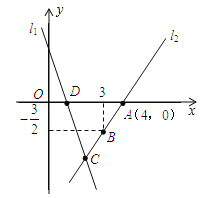
（1）求直线的解析式；

（2）求△ADC的面积；

（3）在直线上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小明家买了一辆小轿车，小明连续记录了一周每天行驶的路程：

请你用学过的统计知识解决下面的问题：

(1)小明家的轿车每月(按30天计算)要行驶多少千米？

(2)若每行驶100千米需汽油8升，汽油每升6.64元，请你算出小明家一年(按12个月计算)的汽油费用大约是多少元(精确到百位)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．

(1)如图 1，等腰直角四边形 ABCD，AB＝BC，∠ABC＝90°.

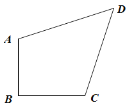
图 1

①若 AB＝CD＝1，AB∥CD，求对角线 BD 的长．

②若 AC⊥BD，求证：AD＝CD；

(2) 如图 2，矩形 ABCD 的长宽为方程－14x+40=0 的两根，其中（BC >AB），点 E 从 A 点出发，以 1 个单位每秒的速度向终点 D 运动；同时点 F 从 C 点出发，以 2 个单位每秒的速度向终点 B 运动，当点 E、F 运动过程中使四边形 ABFE 是等腰直角四边形时，求 EF 的长．