
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
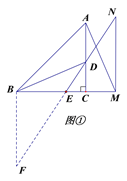
(2)如图①,若点E是BM的中点,求证:MN=AM;
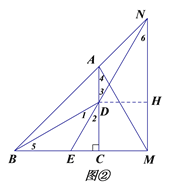
(3)如图②,若点N落在BA的延长线上,求AM的长.

【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】分析:(1)、根据Rt△ACM的勾股定理得出AM的长度;(2)、①过点B作BF⊥BC与NE的延长线交于点F,首先证明△BEF≌△MEN,然后再证明Rt△BDC≌Rt△AMC,从而得出BD=AM,根据角平分线的性质以及平行线的性质得出∠BDF=∠F,从而得出答案;②过点D作DH⊥MN于点H,首先证明四边形CDHM是正方形,然后证明Rt△BDC≌Rt△AMC≌Rt△NDH,根据全等得出∠1=∠2=∠5=30°,根据Rt△BDC的三角函数得出答案.
详解:(1)![]() ;
;
(2)证明:如图①,过点B作BF⊥BC与NE的延长线交于点F,
∵∠ACB=90°,MN∥AC,∴∠FBE=∠NME=90°, 又BE=ME,∠BEF=∠MEN,
∴△BEF≌△MEN,∴BF=MN, ∵CD=CM,BC=AC, ∴Rt△BDC≌Rt△AMC,∴BD=AM,
∵NF平分∠BDC,∴∠BDF=∠FDC, 又由BF∥AC,得:∠F=∠FDC,
∴∠BDF=∠F,∴BD=BF,∴MN=AM.
(3)如图②,过点D作DH⊥MN于点H,
∵MN∥AC,∠ACB=90°,CD=CM,∴四边形CDHM是正方形,
又点N在BA的延长线上,∴△BNM∽△BAC, ∵AC=BC,∴NM=BN,
又MH=CM=DH,∴NH=BC, ∴Rt△BDC≌Rt△AMC≌Rt△NDH, ∴BD=AM=ND,∠5=∠6,
又∠1=∠2,∠2=∠6,∴∠1=∠2=∠5, ∵∠1+∠2+∠5=90°,
∴∠1=∠2=∠5=30°, 在Rt△ABC中,AC=BC,AB=![]() ,∴AC=BC=4,
,∴AC=BC=4,
在Rt△BDC中,![]() ∴AM=
∴AM=![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强在某超市同时购买A,B两种商品共三次,仅有第一次超市将A,B两种商品同时按![]() 折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
A商品的数量(个) | B商品的数量(个) | 购买总费用(元) | |
第一次购买 | 8 | 6 | 930 |
第二次购买 | 6 | 5 | 980 |
第三次购买 | 3 | 8 | 1040 |
(1)求 A,B商品的标价;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A在数轴上对应的数为3,点B对应的数为b,其中A、B两点之间的距离为5
(1)求b的值
(2)当B在A左侧时,一点D从原点O出发以每秒2个单位的速度向左运动,请问D运动多少时间,可以使得D到A、B两点的距离之和为8?
(3)当B在A的左侧时,一点D从O出发以每秒2个单位的速度向左运动,同时点M从B出发,以每秒1个单位的速度向左运动,点N从A出发,以每秒4个单位的速度向右运动;在运动过程中,MN的中点为P,OD的中点为Q,请问MN-2PQ的值是否会发生变化?若发生变化,请说明理由;如果没有变化,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,李明去图书馆借书,下图是他离家的距离 y (千米)与时间 x (分钟)的函数图象,根据图象信息,解答下列问题:
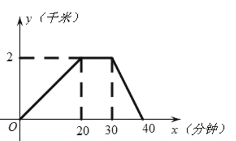
(1)李明家离图书馆有多远?
(2)李明在图书馆停留了多长时间?
(3)李明从图书馆返回家中用了多少时间?
(4)李明全程的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以“绿色生活,美丽家园”为主题的2019年中国北京世界园艺博览会(简称北京世园会)已拉开帷幕,讲述人与自然和谱共生的精彩故事,世园会甲工程队制作园艺造型300个与乙工程队制作园艺造型400个所用时间相等,乙工程队每天比甲工程队多制作10个园艺造型,求甲工程队每天制作园艺造型多少个?
两名同学所列的方程如下:
![]()
根据以上信息,解答下列问题:
(1)小明同学所列方程中的x表示 ,小红同学所列方程中的y表 ;
(2)根据你选择的方程,求出甲工程队每天制作园艺造型多少个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com