
【题目】点A在数轴上对应的数为3,点B对应的数为b,其中A、B两点之间的距离为5
(1)求b的值
(2)当B在A左侧时,一点D从原点O出发以每秒2个单位的速度向左运动,请问D运动多少时间,可以使得D到A、B两点的距离之和为8?
(3)当B在A的左侧时,一点D从O出发以每秒2个单位的速度向左运动,同时点M从B出发,以每秒1个单位的速度向左运动,点N从A出发,以每秒4个单位的速度向右运动;在运动过程中,MN的中点为P,OD的中点为Q,请问MN-2PQ的值是否会发生变化?若发生变化,请说明理由;如果没有变化,请求出这个值.
【答案】(1)![]() ;(2)t=1.75;(3)在运动过程中,MN-2PQ=4恒成立,理由详见解析.
;(2)t=1.75;(3)在运动过程中,MN-2PQ=4恒成立,理由详见解析.
【解析】
(1)根据数轴上两点之间的距离公式即可求解.
(2)根据运动速度可表达出D点坐标,根据D到A、B两点的距离之和为8,可知D点在B的左侧,根据两点之间的距离公式即可求解
(3)根据运动速度可表达出M、D、N点的坐标,根据中点公式求出P、Q坐标进而求出MN、PQ线段长即可求解.
(1)由题意得:![]() ,解得:
,解得:![]()
(2)当B在A左侧时,由(1)可知:![]() ,设点D运动的时间为t秒,则D表示的数为-2t,当D到A、B两点的距离之和为8时,可得D在B左侧,且DB+DA=DB+DB+AB=2DB+5=8,故 DB=1.5,即-2-(-2t)=1.5,解得t=1.75
,设点D运动的时间为t秒,则D表示的数为-2t,当D到A、B两点的距离之和为8时,可得D在B左侧,且DB+DA=DB+DB+AB=2DB+5=8,故 DB=1.5,即-2-(-2t)=1.5,解得t=1.75
(3) 在运动过程中,MN-2PQ=4恒成立,理由如下:
当B在A左侧时,由(1)可知:![]() ,设点D运动的时间为t秒,则
,设点D运动的时间为t秒,则
D表示的数为-2t,M表示的数为-2-t,N表示的数为3+4t;
故MN的中点P表示的数为0.5+1.5t,OD的中点Q表示的数为-t;
则MN-2PQ=[(3+4t)-(-2-t)]-2[(0.5+1.5t)-(-t)]
=5+5t-2(0.5+2.5t)
=5+5t-1-5t
=4


科目:初中数学 来源: 题型:
【题目】小明家买了一辆小轿车,小明连续记录了一周每天行驶的路程:

请你用学过的统计知识解决下面的问题:
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.64元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元(精确到百位).
查看答案和解析>>
科目:初中数学 来源: 题型:
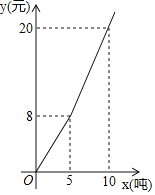
【题目】随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示生活用水费(元).请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过5吨,每吨按 元收取;超过5吨的部分,每吨按 元收取;
(2)请写出居民使用5吨水以内y与x的关系式;
(3)若小明家这个月交水费32元,他家本月用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:

(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由;
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论;
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
(2)如图①,若点E是BM的中点,求证:MN=AM;
(3)如图②,若点N落在BA的延长线上,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2所示,当伞收紧时P与A重合,当伞慢慢撑开时,动点P由A向B移动,当点P到达B时,伞张得最开,此时最大张角∠ECF=150°,已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米CE=CF=18.0分米.
(1)求AP长的取值范围;
(2)当∠CPN=60°,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S.(结果保留![]() )(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
)(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2 000 |
10 | 5 | 2 500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解题过程:
计算:(-15)÷![]() ×6.
×6.
解:原式=(-15)÷![]() ×6(第一步)
×6(第一步)
=(-15)÷(-1)(第二步)
=-15.(第三步)
回答:(1)上面解题过程中有两处错误,第一处是第________步,错误的原因是________________;第二处是第________,错误的原因是________________.
(2)把正确的解题过程写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
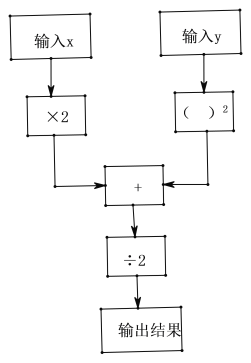
【题目】如图是一个数值转换机的示意图.
(1)请观察示意图,理解运算原理,用代数式表示出来输出的结果 ;
(2)若小倩输入![]() 的值为3,
的值为3,![]() 的值为-2,小旺输入
的值为-2,小旺输入![]() 的值为-3,
的值为-3,![]() 的值为2,若设定输出的结果数大的获胜,他俩谁胜出啦?
的值为2,若设定输出的结果数大的获胜,他俩谁胜出啦?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com