
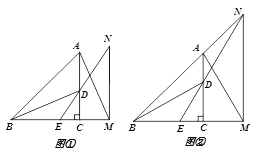
【题目】已知:△ABC是等腰直角三角形,∠ACB=90°,AB=![]() ,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
,将AC边所在直线向右平移,所得直线MN与BC边的延长线相交于点M,点D在AC边上,CD=CM,过点D的直线平分∠BDC,与BC交于点E,与直线MN交于点N,联接AM.
(1)若CM=![]() ,则AM= ;
,则AM= ;
(2)如图①,若点E是BM的中点,求证:MN=AM;
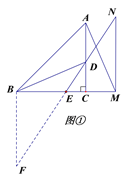
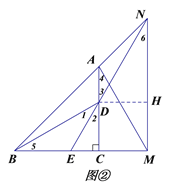
(3)如图②,若点N落在BA的延长线上,求AM的长.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】分析:(1)、根据Rt△ACM的勾股定理得出AM的长度;(2)、①过点B作BF⊥BC与NE的延长线交于点F,首先证明△BEF≌△MEN,然后再证明Rt△BDC≌Rt△AMC,从而得出BD=AM,根据角平分线的性质以及平行线的性质得出∠BDF=∠F,从而得出答案;②过点D作DH⊥MN于点H,首先证明四边形CDHM是正方形,然后证明Rt△BDC≌Rt△AMC≌Rt△NDH,根据全等得出∠1=∠2=∠5=30°,根据Rt△BDC的三角函数得出答案.
详解:(1)![]() ;
;
(2)证明:如图①,过点B作BF⊥BC与NE的延长线交于点F,
∵∠ACB=90°,MN∥AC,∴∠FBE=∠NME=90°, 又BE=ME,∠BEF=∠MEN,
∴△BEF≌△MEN,∴BF=MN, ∵CD=CM,BC=AC, ∴Rt△BDC≌Rt△AMC,∴BD=AM,
∵NF平分∠BDC,∴∠BDF=∠FDC, 又由BF∥AC,得:∠F=∠FDC,
∴∠BDF=∠F,∴BD=BF,∴MN=AM.
(3)如图②,过点D作DH⊥MN于点H,
∵MN∥AC,∠ACB=90°,CD=CM,∴四边形CDHM是正方形,
又点N在BA的延长线上,∴△BNM∽△BAC, ∵AC=BC,∴NM=BN,
又MH=CM=DH,∴NH=BC, ∴Rt△BDC≌Rt△AMC≌Rt△NDH, ∴BD=AM=ND,∠5=∠6,
又∠1=∠2,∠2=∠6,∴∠1=∠2=∠5, ∵∠1+∠2+∠5=90°,
∴∠1=∠2=∠5=30°, 在Rt△ABC中,AC=BC,AB=![]() ,∴AC=BC=4,
,∴AC=BC=4,
在Rt△BDC中,![]() ∴AM=
∴AM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD//EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由。
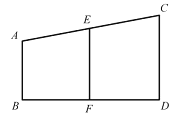
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB=_______________.(____________________)
∴∠ABD+∠CDB=180°
∴AB∥____________(____________________)
又∠A与∠AEF互补(____________________)
∴∠A+∠AEF=___________(____________________)
∴AB//___________(____________________)
∴CD//EF(____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
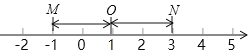
【题目】在数轴上,把表示数1的点称为基准点,记作点O,对于两个不同的点M和N,若点M、点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图中,点M表示﹣1,点N表示3,它们与基准点O的距离都是2个单位长度,点M与点N互为基准变换点.对点A进行如下操作,先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动4个得长度得到点B,若点A与点B互为基准变换点,则点A表示的数为_____.
,再把所得数表示的点沿着数轴向左移动4个得长度得到点B,若点A与点B互为基准变换点,则点A表示的数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动时心跳速率通常和人的年龄有关。用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,则![]() .
.

(1)正常情况下,一个14岁的少年运动时所能承受的每分钟心跳的最高次数是多少?
(2)当一个人的年龄增加10岁时,他运动时承受的每分钟心跳最高次数有何变化?变化次数是多少?
(3)一个45岁的人运动时,10秒心跳次数为22次,请问他有危险吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在纸面上有一条数轴
![]()
操作一:
折叠数轴,使表示1的点与表示-1的点重合,则表示-5的点与表示 的点重合.
操作二:
折叠数轴,使表示1的点与表示3的点重合,在这个操作下回答下列问题:①表示-2的点与表示 的点重合;
②若数轴上A,B两点的距离为7(A在B的左侧),且折叠后A,B两点重合,则点A表示的数为 ,
点B表示的数为
查看答案和解析>>
科目:初中数学 来源: 题型:
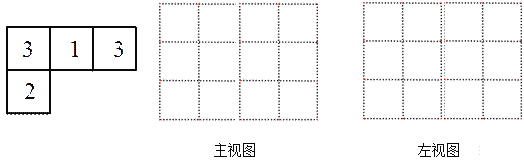
【题目】由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置的正方体个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com