
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论. 
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2= . ( . ),
∴AB∥EF( . )
∴∠3= . ( . )
又∠B=∠3(已知)
∴∠B= . (等量代换)
∴DE∥BC( . )
∴∠C=∠AED( . ).
【答案】∠DFE;同角的补角相等;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;同位角相等,两直线平行;两直线平行,同位角相等
【解析】解:∠C与∠AED相等,理由如下: ∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等).
【考点精析】解答此题的关键在于理解对顶角和邻补角的相关知识,掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个,以及对平行线的判定与性质的理解,了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
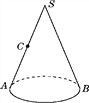
【题目】已知:如图,观察图形回答下面的问题:
(1)此图形的名称为________.
(2)请你与同伴一起做一个这样的物体,并把它沿AS剪开,铺在桌面上,则它的侧面展开图是一个________.
(3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食品,但它又不能直接沿AC爬到C处,只能沿此立体图形的表面爬行,你能在侧面展开图中画出蜗牛爬行的最短路线吗?
(4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
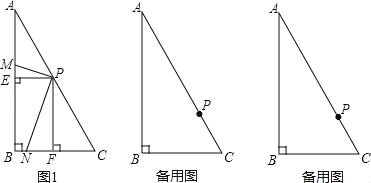
【题目】已知:在Rt△ABC,∠ABC=90°,∠C=60°,现将一个足够大的直角三角板的顶点P放在斜边AC上.
(1)设三角板的两直角边分别交边AB、BC于点M、N.
①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;
②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.
(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB、BC于点M、N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB、BC的延长线与点M、N.
③请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;
④在③的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某文具店进行促销活动,决定将单价为a元的笔记本降价10%销售,降价后的销售价为( )
A. 10%a B. a-10% C. (1-10%)a D. (1+10%)a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com