
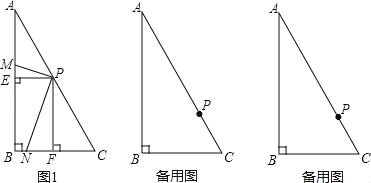
【题目】已知:在Rt△ABC,∠ABC=90°,∠C=60°,现将一个足够大的直角三角板的顶点P放在斜边AC上.
(1)设三角板的两直角边分别交边AB、BC于点M、N.
①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;
②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.
(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB、BC于点M、N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB、BC的延长线与点M、N.
③请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;
④在③的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是 .
【答案】(1)、①△AEP≌△PFC;理由见解析;②、△PFN∽△PEM,PN=![]() PM;理由见解析;(2)、③、答案见解析;④、1cm或5cm
PM;理由见解析;(2)、③、答案见解析;④、1cm或5cm
【解析】
试题分析:(1)、①求出∠AEP=∠B=∠PFC=90°,∠APE=∠C=60°,根据AAS推出两三角形全等即可;②求出AB=![]() BC,求出PE=
BC,求出PE=![]() BC,PF=
BC,PF=![]() AB,推出
AB,推出![]() ,求出∠EPM=∠NPF=90°﹣∠MPF,∠PEM=∠PFN=90°,根据相似三角形的判定推出△PFN∽△PEM,推出
,求出∠EPM=∠NPF=90°﹣∠MPF,∠PEM=∠PFN=90°,根据相似三角形的判定推出△PFN∽△PEM,推出![]() ,即可得出答案;(2)、③过P作PE⊥AB于E,PF⊥BC于F,求出△AEP∽∠PFC,推出
,即可得出答案;(2)、③过P作PE⊥AB于E,PF⊥BC于F,求出△AEP∽∠PFC,推出![]() =2,设CF=x,则PE=2x,求出PF=
=2,设CF=x,则PE=2x,求出PF=![]() x,证△PEM∽△PFN,推出
x,证△PEM∽△PFN,推出![]() 即可;④求出CP=2cm,分为两种情况:第一种情况:当N在线段BC上时,得出△PCN是等边三角形,求出CN=CP=2cm,代入BN=BC﹣CN求出即可;第二种情况:当N在线段BC的延长线上时,求出CN=PC=2cm,代入BN=BC+CN求出即可.
即可;④求出CP=2cm,分为两种情况:第一种情况:当N在线段BC上时,得出△PCN是等边三角形,求出CN=CP=2cm,代入BN=BC﹣CN求出即可;第二种情况:当N在线段BC的延长线上时,求出CN=PC=2cm,代入BN=BC+CN求出即可.
试题解析:(1)、①△AEP≌△PFC,
理由是:∵P为AC中点,∴AP=PC,∵PE⊥AB,PF⊥BC,∠B=90°,∴∠AEP=∠B=∠PFC=90°,
∴PF∥AB,PE∥BC,∴∠APE=∠C=60°,在△AEP和△PFC中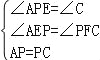 ∴△AEP≌△PFC(AAS).
∴△AEP≌△PFC(AAS).
②、△PFN∽△PEM,PN=![]() PM,
PM,
理由是:∵在Rt△ACB中,∠ABC=90°,∠C=60°,∴AB=![]() BC,
BC,
∵PE∥BC,PF∥AB,P为AC中点,∴E为AB中点,F为BC中点,∴PE=![]() BC,PF=
BC,PF=![]() AB,
AB,
∴![]() ,∵∠PEB=∠B=∠PFB=90°,∴∠EPF=90°,∵∠MPN=90°,
,∵∠PEB=∠B=∠PFB=90°,∴∠EPF=90°,∵∠MPN=90°,
∴∠EPM=∠NPF=90°﹣∠MPF,∵∠PEM=∠PFN=90°,∴△PFN∽△PEM,∴![]() ,∴PN=
,∴PN=![]() PM.
PM.
(2)、③PM=2PN,如图,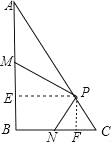
过P作PE⊥AB于E,PF⊥BC于F,∵∠AEP=∠PFC=∠B=90°,∴PE∥BC,∴∠APE=∠C,
∴△AEP∽∠PFC,∴![]() =
=![]() =
=![]() =2,设CF=x,则PE=2x,在Rt△PFC中,∠C=60°,∠PFC=90°,
=2,设CF=x,则PE=2x,在Rt△PFC中,∠C=60°,∠PFC=90°,
∴PF=![]() x,∵在四边形BFPE中,∠BFP=∠B=∠BEP=90°,∴∠EPF=90°,即∠EPM+∠MPF=90°,
x,∵在四边形BFPE中,∠BFP=∠B=∠BEP=90°,∴∠EPF=90°,即∠EPM+∠MPF=90°,
∵∠NPF+∠MPF=90°,∴∠NPF=∠EPM,∵∠MEP=∠PFN=90°,∴△PEM∽△PFN,
∴![]() =
=![]() =
=![]() =
=![]() ,∴PM=
,∴PM=![]() PN.
PN.
④、∵在Rt△ABC中,∠B=90°,∠C=60°,BC=3cm ∴AC=2BC=6cm,∵AP=2PC,∴CP=2cm,
分为两种情况:第一种情况:当N在线段BC上时,如图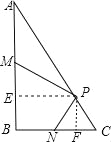
∵△PCN是等腰三角形,∠C=60°,CP=2cm,∴△PCN是等边三角形,∴CN=CP=2cm,
∴BN=BC﹣CN=3cm﹣2cm=1cm;
第二种情况:当N在线段BC的延长线上时,如图,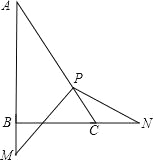
∵∠PCN=180°﹣60°=120°,∴要△PCN是等腰三角形,只能PC=CN,即CN=PC=2cm,
∴BN=BC+CN=3cm+2cm=5cm,即BN的长是1cm或5cm,


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,
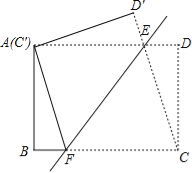
(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论. 
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2= . ( . ),
∴AB∥EF( . )
∴∠3= . ( . )
又∠B=∠3(已知)
∴∠B= . (等量代换)
∴DE∥BC( . )
∴∠C=∠AED( . ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
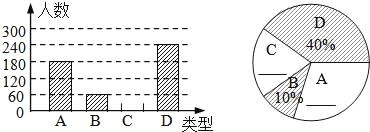
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,![]() 1.7)
1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( ) 
A.130°
B.120°
C.110°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今夏,十堰市王家河村瓜果喜获丰收,果农王二胖收获西瓜20吨,香瓜12吨,现计划租用甲、乙两种货车共8辆将这批瓜果全部运往外地销售,已知一辆甲种货车可装西瓜4吨和香瓜1吨,一辆乙种货车可装西瓜和香瓜各2吨.
(1)果农王二胖如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王二胖应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com