
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.  步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
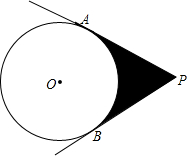 如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
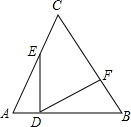 如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.
如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
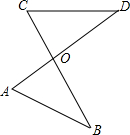 如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.
如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:解答题
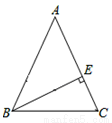
已知:如图,在△ABC中,AB=AC,BE是AC边上的高.
(1)用直尺和圆规作出AB边上的高CD交AB于点D,交BE于点O(要求保留作图痕迹)
(2)判断△OBC是什么三角形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com