
【题目】如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD,垂足为M点.求证: 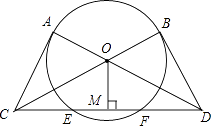
(1)△ACO≌△BDO;
(2)CE=DF.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】直线n与过原点的直线m交于点P,P点的坐标如图所示,直线n与y轴交于点A;若OA=OP;
(1)求A点的坐标;
(2)求直线m,n的函数表达式;
(3)求△AOP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a﹣b=0;
②当﹣2<x<1时,y>0;
③四边形ACBD是菱形;
④9a﹣3b+c>0
你认为其中正确的是( )
A.②③④
B.①②④
C.①③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=a,BC=b,DE垂直平分AB,则(1)△BEC的周长为_____;(2)若EF=BF,BE⊥AC于E,则∠EFC=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |

(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
(1)求证:PB是的切线;
(2)若PB=6,DB=8,求⊙O的半径
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com