
解:(1)线段BD、DE、CE之间的等量关系式是:BD
2+CE
2=DE
2;
理由:∵△ABC中,∠BAC=90°,AB=AC,
∴∠ABD=∠ACE=45°,由旋转的性质可知,△AEC≌△AFB,
∴∠ABF=∠ACE=45°,FB=CE
∴∠FBD=∠ABF+∠ABD=90°旋转角∠FAE=90°,又∠DAE=45°,
故∠FAD=∠FAE-∠DAE=45°,
易证△AFD≌△AED,故FD=DE,
在Rt△FBD中,由勾股定理得:BD
2+BF
2=DF
2;
即:BD
2+CE
2=DE
2.
(2)仿照(1)可证,△AEC≌△AFB,
故BF=CE,△AFD≌△AED,故FD=DE,
∵∠ADE=45°,
∴∠ADF=45°,故∠BDF=90°,
在Rt△BDF中,由勾股定理,得BF
2=BD
2+DF
2,
∴CE
2=BD
2+DE
2.
分析:(1)将△AEC绕A顺时针旋转90°后成△AFB,可证△AEC≌△AFB,故BF=CE,旋转角∠FAE=90°,又∠DAE=45°,故∠FAD=∠FAE-∠DAE=45°,易证△AFD≌△AED,故FD=DE,因为△ABC中,∠BAC=90°,AB=AC,所以∠ABC=∠FAB=45°,从而可得∠FAD=90°,在Rt△FBD中,由勾股定理得线段BD、DE、CE之间的等量关系式;
(2)方法同(2),由∠ADE=45°可得∠ADF=45°,故∠BDF=90°,斜边BF=CE,直角边DF=DE,由勾股定理建立等量关系.
点评:本题考查了旋转的性质,全等三角形的证明及勾股定理的运用.

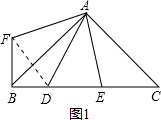
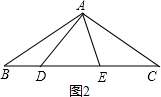
 解:(1)线段BD、DE、CE之间的等量关系式是:BD2+CE2=DE2;
解:(1)线段BD、DE、CE之间的等量关系式是:BD2+CE2=DE2;

 优等生题库系列答案
优等生题库系列答案 如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.
如图,直线AB、CD、MN相交于O,∠DOB=60°,BO⊥FO,OM平分∠DOF.