
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个. 
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵抛物线的对称轴为直线x=﹣1,点B的坐标为(1,0), ∴A(﹣3,0),
∴AB=1﹣(﹣3)=4,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确;
∵抛物线开口向下,
∴a>0,
∵抛物线的对称轴为直线x=﹣ ![]() =﹣1,
=﹣1,
∴b=2a>0,
∴ab>0,所以③错误;
∵x=﹣1时,y<0,
∴a﹣b+c<0,
而a>0,
∴a(a﹣b+c)<0,所以④正确.
故选C.
利用抛物线的对称性可确定A点坐标为(﹣3,0),则可对①进行判断;利用判别式的意义和抛物线与x轴有2个交点可对②进行判断;由抛物线开口向下得到a>0,再利用对称轴方程得到b=2a>0,则可对③进行判断;利用x=﹣1时,y<0,即a﹣b+c<0和a>0可对④进行判断.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F. 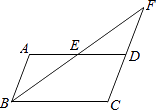
(1)证明:FD=AB;
(2)当ABCD的面积为8时,求△FED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 a+b ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=7,ab=6.求代数式(a-b)的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求该反比例函数和一次函数的解析式.
(2)求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ ![]() <a<
<a< ![]()
⑤b>c.
其中含所有正确结论的选项是( )
A.①③
B.①③④
C.②④⑤
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)14+24﹣8
(2)(﹣3)﹣(﹣2)+(﹣4)
(3)﹣23÷![]() ×(﹣
×(﹣![]() )2
)2
(4)(![]() +
+![]() ﹣
﹣![]() )×(﹣36)
)×(﹣36)
(5)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com